| A | B | C |
|---|---|---|
| 3 | 37.1 | M |
| 4 | 17.4 | M |
| 5 | 26.8 | F |
| 7 | 44.3 | F |
| 5 | 19.7 | F |
14 Hypothesis Testing on Whole Models
A wise man … proportions his belief to the evidence. – David Hume (1711 – 1776), Scottish philosopher
Fitted models describe patterns in samples. Modelers interpret these patterns as indicating relationships between variables in the population from which the sample was drawn. But there is another possibility. Just as the constellations in the night sky are the product of human imagination applied to the random scattering of stars within range of sight, so the patterns indicated by a model might be the result of accidental alignments in the sample.
Deciding how seriously to take the patterns identified by a model is a problem that involves judgment. Are the patterns consistent with well established understanding of how the system works? Are the patterns corroborated by other sources of data? Are the model results sensitive to trivial changes in the model design?
Before undertaking that judgment, it helps to apply a much simpler standard of evidence. The conventional interpretation of a model such as Y ~ A + B + ... is that the variables on the right side of the modeler’s tilde explain the response variable on the left side. The first question to ask is whether the explanation provided by the model is stronger than the “explanation” that would be arrived at if the variables on the right side were random – explanatory variables in name only without any real connection with the response variable Y. If our fitted model can’t do better than than, there isn’t much reason to work on an interpretation.
It’s important to remember that in a hypothesis test, the null hypothesis is about the population. The null hypothesis we are describing here claims that in the population the explanatory variables are unlinked to the response variable. Such a hypothesis does not rule out the possibility that, in a particular sample, the explanatory variables are aligned with the response variable just by chance. The hypothesis merely claims that any such alignment is accidental, due to the randomness of the sampling process, not due to an underlying relationship in the population.
So, for the “whole model test”, sometimes called the “model utility test”, our null hypothesis is:
Null Hypothesis for the Model Utility Test
- \(H_0:\) In the population, the explanatory variables of the model are not associated with the response variable.
In terms of our 4-step process for hypothesis testing, we have now completed step 1. And since step 4 (interpreting the p-value) is essentially the same for any hypothesis, most of the rest of this chapter will focus on steps 2 and 3:
Step 2: Compute the test statistic.
Step 3: Determine the p-value.
14.1 The Permutation Test
The null hypothesis is that the explanatory variables are unlinked with the response variable. One way to see how big a test statistic will be in a world where the null hypothesis holds true is to randomize the explanatory variables in the sample to destroy any relationship between them and the response variable. To illustrate how this can be done in a way that stays true to the sample, consider a small data set:
Imagine that the table has been cut into horizontal slips with one case on each slip. The response variable – say, A – has been written to the left of a dotted line. The explanatory variables B and C are on the right of the dotted line, like this:

To randomize the cases, tear each sheet along the dotted line. Place the right sides – the explanatory variables – on a table in their original order. Then, randomly shuffle the left halves – the response variable – and attach each to a right half.

None of the cases in the shuffle are genuine cases, except possibly by chance. Yet each of the shuffled explanatory variables is true to its distribution in the original sample, and the relationships among explanatory variables – collinearity and multi-collinearity – are also authentic.
Each possible order for the left halves of the cards is called a permutation. A hypothesis test conducted in this way is called a permutation test.
The logic of a permutation test is straightforward. To set up the test, you need to choose a test statistic that reflects some aspect of the system of interest to you.
Here are the steps involved in permutation test:
- Step 2: Calculate the value of the test statistic on the original data.
- Step 3a: Permute the response variable and calculate the test statistic again. Repeat this many times, collecting the results. This gives the distribution of the test statistic under the null hypothesis.
- Step 3b: Read off the p-value as the fraction of the results in Step 3a that are more extreme than the value in Step 2.
14.1.0.1 Height and number of kids
To illustrate, consider a model of heights from Galton’s data and a question Galton didn’t consider: Does the number of children in a family help explain the eventual adult height of the children? Perhaps in families with large numbers of children, there is competition over food, so children don’t grow so well. Or, perhaps having a large number of children is a sign of economic success, and the children of successful families have more to eat.
Now for the permutation test, using the coefficient on nkids as the test statistic:
- Step 2. Calculate the test statistic on the data without any shuffling. As shown above, the coefficient on
nkidsis −0.169.
- Step 3a. Permute and re-calculate the test statistic, many times. One set of 10000 trials gave values of −0.040, 0.037, −0.094, −0.069, 0.062, −0.045, and so on. The distribution is shown in Figure
- Step 3b. The p-value is fraction of times that the values from Step 2 are more extreme than the value of −0.169 from the unshuffled data. As Figure 1 shows, few of the permutations produced an
nkidcoefficient anywhere near −0.169. The p-value is very small, p < 0.001.
Conclusion: the number of kids in a family accounts for more of the children’s heights than is likely to occur with a random explanatory variable.

nkids from the model height ~ 1 + nkids from many permutation trials. Vertical line: the coefficient -0.169 from the unshuffled data.The results of this hypothesis test are consistent with what can learn from a confidence interval for the nkids coefficient in our model.
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 67.80 | 0.30 | 228.96 | 0.0000 |
| nkids | -0.17 | 0.04 | -3.83 | 0.0001 |
For every additional sibling, the family’s children are shorter by about 0.17 inches on average. The confidence interval is \(−0.169 \pm 0.088\), which does not include 0.
14.1.1 A little history
The idea of a permutation test is almost a century old. It was proposed originally by statistician Ronald Fisher (1890-1960). Permutation tests were infeasible for even moderately sized data sets until the 1970s when inexpensive computation became a reality. In Fisher’s day, when computing was expensive, permutation tests were treated as a theoretical notion and actual calculations were performed using algebraic formulas and calculus. Such formulas could be derived for a narrow range of test statistics such as the sample mean, differences between group means, the coefficient of determination \(R^2\), and coefficients in a linear model. Fisher himself derived the sampling distributions of these test statistics. (Fisher 1924) One of them was named after him: the \(F\) distribution.

Although Fisher was an important and influential figure in the development of statistics, his influence was not entirely positive. He was a prominent eugenicist, fought to debunk claims that smoking was linked to cancer, and was known to hold personal grudges against other statisticians (and they against him). These troubling aspects of his history, especially his involvement in the eugenics movement, eventually led the American Statistical Association in 2020 to rename one of its most prestigeous awards that had previously been named in his honor.
14.2 \(R^2\) and the \(F\) Statistic
14.2.1 Limitations on using a model coefficient as a test statistic
Using a model coefficient as a test statistic works well when there is a single quantitative predictor because when that coefficient is 0, the model predicts the same thing for all values of the explanatory variable, just as it would if the explanatory variable had nothing to do with the response variable. But for models with multiple predictors, or with a categorical predictor with more than two levels, the situation is more complicated. No single coefficient tells us everything about whether the model’s predictions depend on the values of the explanatory variables.
14.2.2 Using \(R^2\) as a test statistic
So we need a different test statistic.
The coefficient of determination \(R^2\) measures what fraction of the variance of the response variable is “explained” or “accounted for” or – to put it simply – “modeled” by the explanatory variables. \(R^2\) is a comparison of two quantities: the variance of the fitted model values to the variance of the response variable. \(R^2\) is a single number that puts the explanation in the context of what remains unexplained. It’s a good test statistic for a hypothesis test. \(R^2\) should be near 0 if the explanatory variables have no predictive value, and nearer to 1 or -1 if they do.
14.2.3 The F statistic
Using \(R^2\) as the test statistic in a permutation test would be simple enough. There are advantages, however, to thinking about things in terms of a closely related statistic invented by Fisher and named in honor of him: the \(F\) statistic.
Like \(R^2\), the \(F\) statistic compares the size of the fitted model values to the size of the residuals. But the notion of “size” is somewhat different. Rather than measuring size directly by the variance or by the sum of squares, the \(F\) statistic also takes into account the “size” of the model, measured by the number of model vectors.
To see where \(F\) comes from, consider the random model walk . In a regular random walk, each new step is taken in a random direction. In a random model walk, each “step” consists of adding a new random explanatory term to a model. The “position” is measured as the \(R^2\) from the model.
The starting point of the random model walk is the simple model Y ~ 1 with just \(m=1\) model vector. This model always produces \(R^2 = 0\) because the all-cases-the-same model can’t account for any variance. Taking a “step” means adding a random model vector, x₁, giving the model Y ~ 1 + \(x_1\). Each new step adds a new random vector to the model:
| m | Model |
|---|---|
| 1 | Y ~ 1 |
| 2 | Y ~ \(1+x_1\) |
| 3 | Y ~ \(1+x_1 + x_2\) |
| 3 | Y ~ \(1+x_1 + x_2 + x_3\) |
| 4 | Y ~ \(1+x_1 + x_2 + x_3 + x_{4}\) |
| \(\vdots\) | \(\vdots\) |
| n | Y ~ \(1+x_1 + x_2 + x_3 + \cdots x_{n-1}\) |
Figure Figure 14.5 shows \(R^2\) versus \(m\) for several random model walks in data with n=50 cases. Each successive step adds in its own individual random explanatory term.
All the random walks start at \(R^2 = 0\) for \(m=1\). All of them reach \(R^2 = 1\) when \(m=n\). Adding any more vectors beyond \(m=n\) simply creates redundancy; \(R^2 = 1\) is the best that can be done. Notice that each step increases \(R^2\) – none of the random walks goes down in value as m gets bigger.


The \(R^2\) from a fitted model gives a single point on the model walk that divides the overall walk into two segments, as shown in Figure Figure 14.6. The slope of each of the two segments has a straightforward interpretation. The slope of the segmented labeled “Model” describes the rate at which \(R^2\) is increased by a typical model vector. The slope can be calculated as \(R^2 / (m−1)\).
The slope of the segment labeled “Residuals” describes how adding a random vector to the model would increase \(R^2\). Numerically, the slope is \((1−R^2)/(m−n)\).
From the figure, you can see that a typical model vector increases \(R^2\) much faster than a typical random vector. The \(F\) statistic is the ratio of these two slopes:
\[\begin{align} F & = \frac{\mbox{slope of model segment}}{\mbox{slope of residual segment}} = \frac{R^2 /(m-1) }{ (1-R^2)/(n-m)} \end{align}\]
Because \(R^2 = \frac{SSM}{SST}\), there are several other ways to write this \(F\) statistic:
\[\begin{align} F = \frac{\mbox{slope of model segment}}{\mbox{slope of residual segment}} & = \frac{R^2 /(m-1) }{ (1-R^2)/(n-m)} \\ &= \frac{\frac{SSM}{SST} /(m-1) }{ \frac{RSS}{SST}/(n-m)} \\ &= \frac{SSM /(m-1) }{ RSS/(n-m)} \\ &= \frac{MSM}{MSE} \end{align}\]
In interpreting the \(F\) statistic, keep in mind that if the model vectors were no better than random, \(F\) should be near 1. When \(F\) is much bigger than 1, it indicates that the model terms explain more than would be expected at random. The p-value provides an effective way to identify when \(F\) is “much bigger than 1.”
Calculating the p-value involves knowing the distribution of the \(F\) statistic when the null hypothesis is true. There are two ways we can do this:
We can use simulations to generate many values of \(F\) after permuting the response variable as described above, or
When the linear model assumptions are met, the \(F\) statistics follow a known distribution, known as the F-distribution.
The family of F-distributions has two paramters:
The number \(m-1\) in the numerator of \(F\) counts how many model terms there are other than the intercept. In standard statistical nomenclature, this is called the degrees of freedom of the numerator
The number \(n−m\) in the denominator of \(F\) counts how many random terms would need to be added to make a “perfect” fit to the response variable. This number is called the degrees of freedom of the denominator.
Either way, we will rely on the computer to turn our observed test statistic into a p-value.
14.2.3.1 The shape of \(F\)
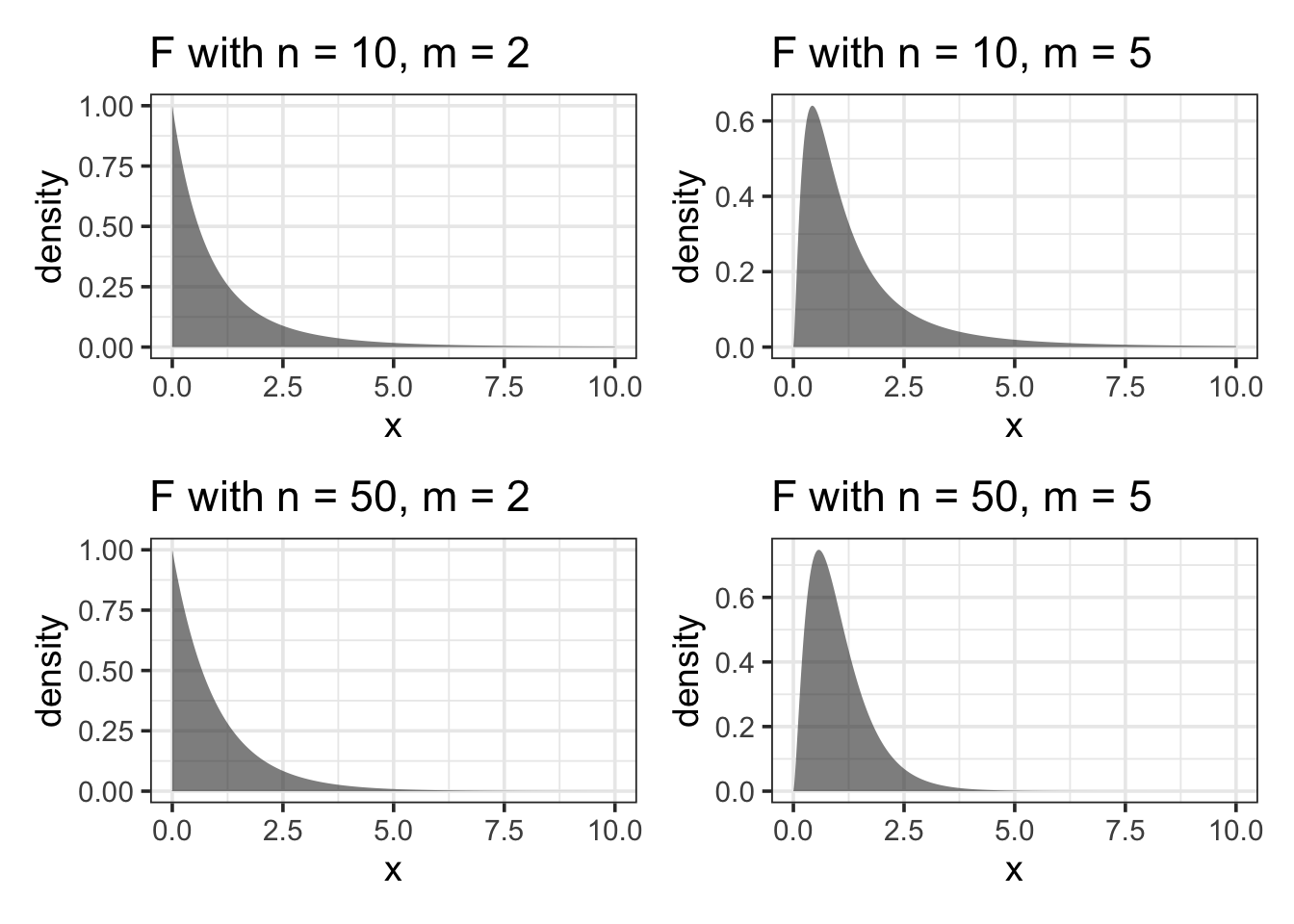
For each combination of these two degrees of freedom values (\(m-1\) and \(n-m\)), we get a different distribution from the family of F distributions. A few examples are shown in Figure Figure 14.7.
Despite their different shapes, the \(F\) distributions are all centered on 1. (In contrast, distributions of \(R^2\) change shape substantially with \(m\) and \(n\).) This steadiness in the \(F\) distribution makes it easier to interpret an \(F\) statistic by eye since a value near 1 is a plausible outcome from the null hypothesis. (The meaning of “near” reflects the width of the distribution: When \(n\) is much bigger than \(m\), the the \(F\) distribution has mean 1 and standard deviation that is roughly \(\sqrt{2/m}\).)

14.3 ANOVA Tables
The \(F\) statistic compares the variation that is explained by the model to the variation that remains unexplained. Doing this involves taking apart the variation; partitioning it into a part associated with the model and a part associated with the residuals. We’ve seen this idea before, but it will become even more important going forward.
Such partitioning of variation is fundamental to statistical methods. When done in the context of linear models, this partitioning is given the name analysis of variance – ANOVA for short. This name stays close to the dictionary definition of “analysis” as “the process of separating something into its constituent elements.” (“New Oxford American Dictionary” 2015)
The analysis of variance is often presented in a table called an ANOVA table. There are several ways that these tables are constructed, depending on which features of the partitioning of variance are most important to the person creating the table.
Example 14.1 (Height and number of kids) Let’s take a look at the ANOVA table for our height ~ 1 + nkids model using Galton’s data.
| df | SS | MS | F | p_value | |
|---|---|---|---|---|---|
| model | 1 | 185.4636 | 185.46365 | 14.66737 | 0.000137178 |
| residuals | 896 | 11329.5987 | 12.64464 |
Notice that the p-value in the ANOVA table is the same p-value that appears in a summary of the regression coefficients:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 67.7997464 | 0.29612327 | 228.9578 | 0.000000000 |
| nkids | -0.1693416 | 0.04421682 | -3.8298 | 0.000137178 |
That’s because (in this case), they are testing the same null hypothesis:
- \(H_0:\) The number of children in a family is not associated with the height of the children when they are adults.
That hypothesis is equivalent to saying
- \(H_0\): The
nkidscoefficient (in the population) from theheight ~ 1 + nkidsmodel is 0.
We’ll learn more about this sort of null hypothesis (the hypothesis that a model coefficient is 0) in the next chapter. For now, just note that we get the same p-value either way here only because our model is so simple. In models with additional terms, this will no longer be the case.
Note that although we have established a statistical association between the number of children in a family and the height of kids, this statistical result does not answer the question of why there is such an association.
Example 14.2 (Is height genetically determined?) Francis Galton’s study of height in the late 1800s was motivated by his desire to quantify genetic inheritance. In 1859, Galton read Charles Darwin’s On the Origin of Species in which Darwin first put forward the theory of natural selection of heritable traits. (Galton and Darwin were half-cousins, sharing the same grandfather, Erasmus Darwin.)
| Charles Darwin (1809-1882) | Francis Galton (1822-1911) |
The publication of Origin of Species preceded by a half-century any real understanding of the mechanism of genetic heritability. Today, of course, even elementary-school children hear about DNA and chromosomes, but during Darwin’s life these ideas were unknown. Darwin himself thought that traits were transferred from the parents to the child literally through the blood, with individual traits carried by “gemmules.” Galton tried to confirm this experimentally by doing blood-mixing experiments on rabbits; these were unsuccessful at transferring traits.
By collecting data on the heights of adult children and their parents, Galton sought to quantify to what extent height is determined genetically. Galton faced the challenge that the appropriate statistical methods had not yet been developed – he had to start down this path himself. In a very real sense, the development of ANOVA by Ronald Fisher in the early part of the twentieth century was a direct outgrowth of Galton’s work.
Had he been able to, here is the ANOVA report that Galton might have generated. The report summarizes the extent to which height is associated with inheritance from the mother and the father and by the genetic trait sex, using the model height ~ 1 + sex + mother + father.
| df | SS | MS | F | p_value | |
|---|---|---|---|---|---|
| model | 3 | 7365.900 | 2455.300112 | 529.0317 | 0 |
| residuals | 894 | 4149.162 | 4.641121 |
The \(F\) value is huge – typical values for this \(F\) distribution are smaller than 5 – and accordingly the p-value is very small: the three terms in our model are clearly explaining much more of height than random vectors would be likely to do.

If Galton had had access to modern statistical approaches – even those from as long ago as the middle of the twentieth century – he might have wondered how to go further, for example how to figure out
whether the heights of the parents matter much or if the only important part of the model is the sex of the individual.
whether the mother and father each contribute to height, or whether it is a trait that comes primarily from one parent.
Answering such questions involves partitioning the variance not merely between the model terms and the residual but among the individual model terms. This is the subject of Chapter 15.
14.3.1 \(F\) and \(R^2\)
The \(R^2\) value doesn’t appear explicitly in the ANOVA table, but it’s easy to calculate since the report does give SSM and RSS (aka SSE). We can add these to get SST, and sometimes an additional row is presented in the ANOVA table that includes this value:
| df | SS | MS | F | p_value | |
|---|---|---|---|---|---|
| model | 3 | 7365.900 | 2455.300112 | 529.0317 | 0 |
| residuals | 894 | 4149.162 | 4.641121 | ||
| total | 897 | 11515.062 | 12.837305 |
In the Galton example,
\[ R^2 = \frac{SSM}{SST} = \frac{7366}{11515} = 0.64 \]
The mean square in each row is the sum of squares divided by the degrees of freedom. The Mean Sq value in the last row of the expanded table is just the variance of the response variable.
Finally, the \(F\) value is converted to a p-value either by simulation or by using the \(F\) distribution with the indicated degrees of freedom in the numerator and the denominator.
The values of \(R^2\) and \(F\) (and the associated degrees of freedom and p-value) also appear in many regression summary reports:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.34476 2.74696 5.586 3.08e-08
sexM 5.22595 0.14401 36.289 < 2e-16
mother 0.32150 0.03128 10.277 < 2e-16
father 0.40598 0.02921 13.900 < 2e-16
Residual standard error: 2.154 on 894 degrees of freedom
Multiple R-squared: 0.6397, Adjusted R-squared: 0.6385
F-statistic: 529 on 3 and 894 DF, p-value: < 2.2e-1614.4 Multiple Comparisons
The p-value is a useful format for summarizing the strength of evidence that the data provide. But statistical evidence, like any other form of evidence, needs to be interpreted in context.
Keep in mind that a hypothesis test, particularly when \(p\) is near the conventional \(p<0.05\) threshold for rejection of the null, is a very weak standard of evidence. Failure to reject the null may just mean that there isn’t enough data to reveal the patterns, or that important explanatory variables have not been included in the model.
But even when the p-value is below 0.05, it needs to be interpreted in the context within which the tested hypothesis was generated. Often, models are used to explore data, looking for relationships among variables. The hypothesis tests that stem from such an exploration can give misleadingly low p-values. To illustrate, consider an analogous situation in the world of crime. Suppose there were 20 different genetic markers evenly distributed through the population. A crime has been committed and solid evidence found on the scene shows that the perpetrator has a particular genetic marker, M, found in only 5% of the population. The police fan out through the city, testing passersby for the M marker. A man with M is quickly found and arrested.
Should he be convicted based on this evidence? Of course not. That this specific man should match the crime marker is unlikely, a probability of only 5%. But by testing large numbers of people who have no particular connection to the crime, it’s a guarantee that someone who matches will be found.
Now suppose that eyewitnesses had seen the crime at a distance. The police arrived at the scene and quickly cordoned off the area. A man, clearly nervous and disturbed, was caught trying to sneak through the cordon. Questioning by the police revealed that he didn’t live in the area. His story for why he was there did not hold up. A genetic test shows he has marker M. This provides much stronger, much more credible evidence. The physical datum of a match is just the same as in the previous scenario, but the context in which that datum is set is much more compelling.
The lesson here is that the p-value needs to be interpreted in context. The p-value itself doesn’t reveal that context. Instead, the story of the research project comes into play. Have many different models been fitted to the data? If so, then it’s likely that one or more of them may have \(p < 0.05\) even if the explanatory variables are not linked to the response.
It’s a grave misinterpretation of hypothesis testing to treat the p-value as the probability that the null hypothesis is true. Remember, the p-value is based on the assumption that the null hypothesis is true. A low p-value may call that assumption into doubt, but that doubt needs to be placed into the context of the overall situation.
Consider the unfortunate researcher who happens to work in a world where the null hypothesis is always true. In this world, each study that the researcher performs will produce a p-value that is effectively a random number equally likely to be anywhere between 0 and 1. If this researcher performs many studies, it’s highly likely that one or more of them will produce a p-value less than 0.05 even though the null is true.
Tempting though it may be to select a single study from the overall set based on its low p-value, it’s a mistake to claim that this isolated p-value accurately depicts the probability of the null hypothesis. Statistician David Freedman writes, “Given a significant finding … the chance of the null hypothesis being true is ill-defined – especially when publication is driven by the search for significance.” (Freedman 2008)
14.4.1 Dealing with multiple comparisons
One approach to dealing with multiple tests is to adjust the threshold for rejection of the null to reflect the multiple possibilities that chance has to produce a small p-value. A simple and conservative method for adjusting for multiple tests is the Bonferroni correction. Suppose you perform \(k\) different tests. The Bonferroni correction adjusts the threshold for rejection downward by a factor of \(1/k\). For example, if you perform 15 hypothesis tests, rather than rejecting the null at a level of \(0.05\), your threshold for rejection should be \(0.05/15 = 0.0033\).
Another strategy is to treat multiple testing situations as “hypothesis generators.” Tests that produce low p-values are not to be automatically deemed as significant but as worthwhile candidates for further testing (Saville 1990). Go out and collect a new sample, independent of the original one. Then use this sample to perform exactly one hypothesis test: re-testing the model whose low p-value originally prompted your interest. This common-sense procedure is sometimes called a replication study because it is attempting to replicate a previous result.
When reading work from others, it can be hard to know for sure how many hypotheses were (or might have been) considered by the researchers. For this reason, researchers value prospective studies, where the data are collected after the hypothesis has been framed. In contrast, in retrospective studies, where data that have already been collected are used to test the hypothesis, there is a possibility that the same data used to form the hypothesis are also being used to test it. Retrospective studies are often disparaged for this reason, although really the issues are how many tests were performed using the same data, whether an appropriate adjustment was made to the p-value threshold, and whether the data helped shape the hypotheses being tested. (Retrospective studies also have the disadvantage that the data being analyzed might not have been collected in a way that optimally addresses the hypothesis. For example, important covariates might have been neglected.)
Example 14.3 (Multiple Jeopardy) You might be thinking: Who would conduct multiple tests, effectively shopping around for a low p-value? It happens all the time, even in situations where wrong conclusions have important implications.1
To illustrate, consider the procedures adopted by the US Government’s Office of Federal Contract Compliance Programs when auditing government contractors to see if they discriminate in their hiring practices. The OFCCP requires contractors to submit a report listing the number of applicants and the number of hires broken down by sex, by several racial/ethnic categories, and by job group. In one such report, there were 9 job groups (manager, professional, technical, sales workers, office/clerical, skilled crafts, operatives, laborers, service workers) and 6 discrimination categories (Black, Hispanic, Asian/Pacific Islander, American Indian/American Native, females, and people with disabilities).
According to the OFCCP operating procedures (Federal Contract Compliance Programs 1993, revised 2002), a separate hypothesis test with a rejection threshold of about 0.05 is to be undertaken for each job group and for each discrimination category, for example, discrimination against Black managers or against female sales workers. This corresponds to 54 different hypothesis tests. Rejection of the null in any one of these tests triggers punitive action by the OFCCP. Audits can occur annually, so there is even more potential for repeated testing.
Such procedures are not legitimately called hypothesis tests; they should be treated as screening tests meant to identify potential problem areas which can then be confirmed by collecting more data. A legitimate hypothesis test would require that the threshold be adjusted to reflect the number of tests conducted, or that a pattern identified by screening in one year has to be confirmed in the following year.
Example 14.4 (Do green jelly beans cause acne?) For a more lighthearted example (with an important point) see this XKCD comic.

14.5 Significance vs Substance
It’s very common for people to misinterpret the p-value as a measure of the strength of a relationship, rather than as a measure for the evidence that the data provide that the relationship exists at all. Even when a relationship is very slight, as indicated by model coefficients or \(R^2\), the evidence for it can be very strong so long as there are enough cases.
Suppose, for example, that you are studying how long patients survive after being diagnosed with a particular disease. The typical survival time is 10 years, with a standard deviation of 5 years. In your research, you have identified a genetic trait that explains some of the survival time: modeling survival by the genetics produces an \(R^2\) of 0.01. Taking this genetic trait into account makes the survival time more predictable; it reduces the standard deviation of survival time from 5 years to 4.975 years. Big deal! The fact is, an \(R^2\) of 0.01 does not reduce uncertainty very much; it leaves 99 percent of the variance unaccounted for.
To see how the \(F\) statistic stems from both \(R^2 = 0.01\) and the sample size n, we can rewrite the formula for \(F\) from Equation 14.1:
\[ \begin{aligned} F &= \frac{R^2 /(m-1) }{ (1-R^2)/(n-m)} \\ &= \frac{n-m}{m-1}\cdot \frac{R^2}{1-R^2} \\ & = \mbox{sample size} \cdot \mbox{substance} \end{aligned} \]
The ratio \(R^2/(1-R^2)\) is a reasonable way to measure the substance of the result: how forceful the relationship is. The ratio \((n-m)/(m-1)\) reflects the amount of data (and the complexity of the model). Any relationship, even one that lacks practical substance, can be made to give a large \(F\) value so long as \(n\) is big enough. For example, taking \(m=2\) in your genetic trait model, a small study with \(n=100\) gives an \(F\) value of approximately 1: not significant. But if \(n=1000\) cases were collected, the \(F\) value would become a hugely significant \(F=10\). When used in a statistical sense to describe a relationship, the word “significant” does not mean important or substantial. It merely means that there is evidence that the relationship did not arise purely by chance from random variation in the sample.
Example 14.5 (The Significance of Finger Lengths) The example in Section 14.4 commented on a study that found \(R^2 = 0.044\) for the relationship between finger-length ratios and aggressiveness. The relationship was hyped in the news media as the “key to aggression.” (BBC News, 2005/03/04) The researchers who published the study (Bailey and Hurd 2005) didn’t characterize their results in this dramatic way. They reported merely that they found a statistically significant result, that is, p-value of \(0.028\). The small p-value stems not from a forceful correlation but from number of cases; their study, at \(n=134\), was large enough to produce a value of \(F\) bigger than 4 even though the “substance”, \(R^2/(1−R^2)\), is only 0.046. (\(R^2 = 0.044\).)
The researchers were careful in presenting their results and gave a detailed presentation of their study. They described their use of four different ways of measuring aggression: physical, hostility, verbal, and anger. These four scales were each used to model finger-length ratio for men and women separately. Here are the p-values they report:
| Sex | Scale | \(R^2\) | p-value |
|---|---|---|---|
| Males | Physical | 0.044 | 0.028 |
| Hostility | 0.016 | 0.198 | |
| Verbal | 0.008 | 0.347 | |
| Anger | 0.001 | 0.721 | |
| Females | Physical | 0.010 | 0.308 |
| Hostility | 0.001 | 0.670 | |
| Verbal | 0.001 | 0.778 | |
| Anger | 0.000 | 0.887 |
Notice that only one of the eight p-values is below the 0.05 threshold. The others seem randomly scattered on the interval 0 to 1, as would be expected if there were no relationship between the finger-length ratio and the aggressiveness scales. A Bonferroni correction to account for the eight tests gives a rejection threshold of 0.05/8 = 0.00625. None of the tests satisfies this threshold.
See Section 13.9 for another example.↩︎