13 The Logic of Hypothesis Testing
Extraordinary claims demand extraordinary evidence. – Carl Sagan (1934-1996), astronomer
The test of a first-rate intelligence is the ability to hold two opposing ideas in mind at the same time and still retain the ability to function. – F. Scott Fitzgerald (1896-1940), novelist
A hypothesis test is a standard format for assessing statistical evidence. It is ubiquitous in scientific literature, most often appearing in the form of statements of statistical significance and notations like “p < 0.01” that pepper scientific journals.
Hypothesis testing involves a substantial technical vocabulary: null hypotheses, alternative hypotheses, test statistics, significance, p-values, power, and so on. The last section of this chapter lists the terms and gives definitions.
Hypothesis testing has become a bit controversial in recent years, with some journals even banning the use of hypothesis tests. This isn’t because there is something wrong with the tests themselves as much as because they have often been misused, abused, or just misunderstood. The recent discussion of hypothesis testing led the the American Statistical Association to publish a statement on statistical significance and p-values to address some of the concerns and to offer guidelines for using hypothesis tests correctly. Among their enumerated points is
3. Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
In other words, we cannot just look at a p-value and get the answer to our question. It is important to understand what hypothesis tests are, what they do and do not tell us, and how various aspects of the study design factor into interpreting the results.
The technical aspects of hypothesis testing arise because it is a highly formal and quite artificial way of reasoning. This isn’t a criticism. Hypothesis testing is this way because the “natural” forms of reasoning are inappropriate. To illustrate why, consider an example.
13.1 Example: Ups and downs in the stock market
The stock market’s ups and downs are reported each working day. Some people make money by investing in the market, some people lose. Is there reason to believe that there is a trend in the market that goes beyond the random-seeming daily ups and downs?
Figure 13.1 shows the closing price of the Dow Jones Industrial Average stock index for a period of about 10 years up until just before the 2008 recession, a period when stocks were considered a good investment. It’s evident that the price is going up and down in an irregular way, like a random walk. But it’s also true that the price at the end of the period is much higher than the price at the start of the period.

13.1.1 Formulating a question data can answer
Is there a trend or is this just a random walk? It’s undeniable that there are fluctuations that look something like a random walk, but is there a trend buried under the fluctuations?
As phrased, the question contrasts two different possible hypotheses. The first is that the market is a pure random walk. The second is that the market has a systematic trend in addition to the random walk.
The natural question to ask is this: Which hypothesis is right?
Each of the hypotheses is actually a model: a representation of the world for a particular purpose. But each of the models is an incomplete representation of the world, so each is wrong.
It’s tempting to rephrase the question slightly to avoid the simplistic idea of right versus wrong models: Which hypothesis is a better approximation to the real world? That’s a nice question, but how would we answer it in practice? To say how each hypothesis differs from the real world, you need to know already what the real world is like: Is there a trend in stock prices or not? That approach won’t take you anywhere.
Here is another idea: Which hypothesis gives a better match to the data? This seems a simple matter: fit each of the models to the data and see which one gives the better fit. But recall that even junk model terms can lead to smaller residuals. In the case of the stock market data, it happens that the model that includes a trend will almost always give smaller residuals than the pure random walk model, even if the data really do come from a pure random walk.
The logic of hypothesis testing avoids these problems. The basic idea is to avoid having to reason about the real world by setting up a hypothetical world that is completely understood. The observed patterns of the data are then compared to what would be generated in the hypothetical world. If they don’t match well enough, then there is reason to doubt that the data support the hypothesis.
13.1.2 Formalizing as a hypothesis test
To illustrate the basic structure of a hypothesis test, here is one using the stock-market data.
The test statistic is a number that is calculated from the data and summarizes the observed patterns of the data. A test statistic might be a model coefficient or an \(R^2\) value or something else. For the stock market data, it’s sensible to use as the test statistic the start-to-end dollar difference in prices over the 2500-day period. The observed value of this test statistic is $5446 – the DJIA stocks went up by this amount over the 10-year period.
Here is the big question: Could that have happened just by pure chance according to a random-walk model with no underlying trend? If so, then we have no reason to suspect anything more than random chance. But if it would be highly unusual for the random-walk model to lead to such a large increase, then we might conclude that something else is going on here.
In order to carry out the hypothesis test, you construct a conjectural or hypothetical world in which the hypothesis is true. You can do this by building a simulation of that world and generating data from the simulation. Traditionally, such simulations have been implemented using probability theory and algebra to carry out the calculations of what results are likely in the hypothetical world. It’s also possible to use direct computer simulation of the hypothetical world. Either method will work.
The challenge is to create a hypothetical world that is relevant to the real world. It would not, for example, be relevant to hypothesize that stock prices never change, nor would it be relevant to imaging that they change by an unrealistic amount. Later chapters will introduce a few techniques for doing this in statistical models. For this stock-price hypothesis, we’ll imagine a hypothetical world in which prices change randomly up and down by the same daily amounts that they were seen to change in the real world, but are equally likely to go up as to go down. (In the actual data, they went up more than they went down.)
In other words, our simulation will randomly sample a change (using the actual amounts of change observed) and then flip a coin to decide if the market goes up or down by that amount. If repeat this simulation many times, sometimes the simulated market will go up, sometimes it will go down. Sometimes the overall change will be larger, sometimes it will be smaller. But how often will it be as large as the $5446 that we observed in the actual data? If a change that large happens reasonably often, then the data are consistent with the random walk hypothesis. If a change that large almost never happens in our simulations, then it would seem that the data are not consistent with the random walk hypothesis.
Figure 13.2 shows a few examples of stock prices in the hypothetical world where prices are equally likely to go up or down each day by the same daily percentages seen in the actual data.
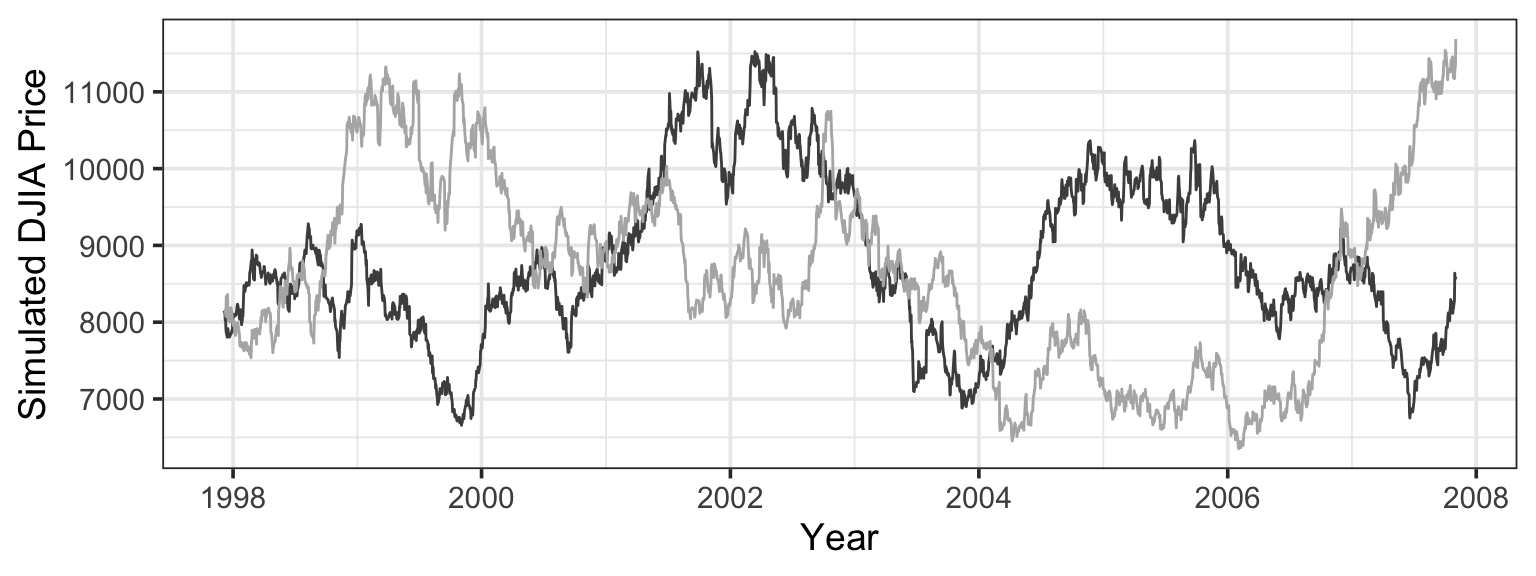
By generating many such simulations, and measuring from each individual simulation the start-to-end change in price, you get an indication of the range of likely outcomes in the hypothetical world. This is shown in Figure 13.3, which also shows the value observed in the real world – a price increase of $5446.

Since the observed start-to-end change in price is well within the possibilities generated by the simulation, we’ll say that the data are consistent with that hypothesis. The formal lingo uses a double negative: We fail to reject the hypothesis. This doesn’t mean the random walk hypothesis is true; other hypothesis may also be consistent with the data. But these data don’t provide us with enough evidence to rule out the random walk hypothesis.
13.2 Inductive and Deductive Reasoning
Hypothesis testing involves a combination of two different styles of reasoning: deduction and induction. In the deductive part, the hypothesis tester makes an assumption about how the world works and draws out, deductively, the consequences of this assumption: what the distribution of the test statistic should be if the hypothesis is true. For instance, the hypothesis that stock prices are a random walk was translated into a statement of the probability distribution of the start-to-end price difference.
In the inductive part of a hypothesis test, the tester compares the actual observations to the deduced consequences of the assumptions and decides whether the observations are consistent with them.
13.2.1 Deductive Reasoning
Deductive reasoning involves a series of rules that bring you from given assumptions to the consequences of those assumptions. For example, here is a form of deductive reasoning called a syllogism:
- Assumption 1: No healthy food is fattening.
- Assumption 2: All cakes are fattening.
- Conclusion: No cakes are healthy.
The actual assumptions involved here are questionable, but the pattern of logic is correct. If the assumptions were right, the conclusion would be right also.
Deductive reasoning is the dominant form in mathematics. It is at the core of mathematical proofs and lies behind the sorts of manipulations used in algebra. For example, the equation 3x + 2 = 8 is a kind of assumption. Another assumption, known to be true for numbers, is that subtracting the same amount from both sides of an equation preserves the equality. So you can subtract 2 from both sides to get 3x = 6. The deductive process continues – divide both sides by 3 – to get a new statement, x = 2, that is a logical consequence of the initial assumption. Of course, if the assumption 3x + 2 = 8 was wrong, then the conclusion x = 2 would be wrong too.
The contrapositive is a way of recasting an assumption in a new form that will be true exactly when the original assumption is true. For example, suppose the original assumption is, “My car is red.” Another way to state this assumption is as a statement of implication, an if-then statement:
- Assumption: If it is my car, then it is red.
To form the contrapositive, you re-arrange the assumption to produce another statement:
- Contrapositive If it is not red, then it is not my car.
Any assumption of the form “if [statement 1] then [statement 2]” has a contrapositive. In the example, statement 1 is “it is my car.” Statement 2 is “it is red.” The contrapositive looks like this:
- Contrapositive: If [negation of statement 2] then [negation statement 1].
The contrapositive is, like algebraic manipulation, a re-rearrangement: reverse and negate. Reversing means switching the order of the two statements in the if-then structure. Negating a statement means saying the opposite. The negation of “it is red” is “it is not red.” The negation of “it is my car” is “it is not my car.” (It would be wrong to say that the negation of “it is my car” is “it is your car.” Clearly it’s true that if it is your car, then it is not my car. But there are many ways that the car can be not mine and yet not be yours. There are, after all, many other people in the world than you and me!)
Contrapositives often make intuitive sense to people. That is, people can see that a contrapositive statement is correct even if they don’t know the name of the logical re-arrangement. For instance, here is a variety of ways of re-arranging the two clauses in the assumption, “If that is my car, then it is red.” Some of the arrangements are logically correct, and some aren’t.
Original Assumption: If it is my car, then it is red.
Negate first statement: If it is not my car, then it is red.
Wrong. Other people can have cars that are not red.
Negate only second statement: If it is my car, then it is not red.
Wrong. The statement contradicts the original assumption that my car is red.
Negate both statements: If it is not my car, then it is not red.
Wrong. Other people can have red cars.
Reverse statements: If it is red, then it is my car.
Wrong. Apples are red and they are not my car. Even if it is a car, not every red car is mine.
Reverse and negate first: If it is red, then it is not my car.
Wrong. My car is red.
Reverse and negate second: If it is not red, then it is my car.
Wrong. Oranges are not red, and they are not my car.
Reverse and negate both – the contrapositive: If it is not red, then it is not my car.
Correct.
13.2.2 Inductive Reasoning
In contrast to deductive reasoning, inductive reasoning involves generalizing or extrapolating from a set of observations to conclusions. An observation is not an assumption: it is something we see or otherwise perceive. For instance, you can go to Australia and see that kangaroos hop on two legs. Every kangaroo you see is hopping on two legs. You conclude, inductively, that all kangaroos hop on two legs.
Inductive conclusions are not necessarily correct. There might be one-legged kangaroos. That you haven’t seen them doesn’t mean they can’t exist. Indeed, Europeans believed that all swans are white until explorers discovered that there are black swans in Australia.
Suppose you conduct an experiment involving 100 people with fever. You give each of them aspirin and observe that in all 100 the fever is reduced. Are you entitled to conclude that giving aspirin to a person with fever will reduce the fever? Not really. How do you know that there are no people who do not respond to aspirin and who just happened not be be included in your study group?
Perhaps you’re tempted to hedge by weakening your conclusion: “Giving aspirin to a person with fever will reduce the fever most of the time.” This seems reasonable, but it is still not necessarily true. Perhaps the people in you study had a special form of fever-producing illness and that most people with fever have a different form.
By the standards of deductive reasoning, inductive reasoning does not work. No reasonable person can argue about the deductive, contrapositive reasoning concerning the red car. But reasonable people can very well find fault with the conclusions drawn from the study of aspirin.
Here’s the difficulty. If you stick to valid deductive reasoning, you will draw conclusions that are correct given that your assumptions are correct. But how can you know if your assumptions are correct? How can you make sure that your assumptions adequately reflect the real world? At a practical level, most knowledge of the world comes from observations and induction.
The philosopher David Hume noted the everyday inductive “fact” that food nourishes us, a conclusion drawn from everyday observations that people who eat are nourished and people who do not eat waste away. Being inductive, the conclusion is suspect. Still, it would be a foolish person who refuses to eat for want of a deductive proof of the benefits of food.
Inductive reasoning may not provide a proof, but it is nevertheless useful.
13.3 The Null Hypothesis
A key aspect of hypothesis testing is the choice of the hypothesis to test. The stock market example involved testing the random-walk hypothesis rather than the trend hypothesis. Why? After all, the hypothesis of a trend is more interesting than the random-walk hypothesis; it’s more likely to be useful if true.
It might seem obvious that the hypothesis you should test is the hypothesis that you are most interested in. But this is wrong.
In a hypothesis test one assumes that the hypothesis to be tested is true and draws out the consequences of that assumption in a deductive process. This can be written as an if-then statement:
If hypothesis H is true, then the test statistic S will be drawn from a probability distribution P.
For example, in the stock market test, the assumption that the day-to-day price change is random leads to the conclusion that the test statistic – the start-to-end price difference – will be a draw from the distribution shown in Figure 13.3.
The inductive part of the test involves comparing the observed value of the test statistic S to the distribution P. There are two possible outcomes of this comparison:
- Agreement: S is a plausible outcome from P.
- Disagreement: S is not a plausible outcome from P.
Suppose the outcome is agreement between S and P. What can be concluded? Not much. Recall the statement “If it is my car, then it is red.” An observation of a red car does not legitimately lead to the conclusion that the car is mine. For an if-then statement to be applicable to observations, one needs to observe the if-part of the statement, not the then-part.
An outcome of disagreement gives a more interesting result, because the contrapositive gives logical traction to the observation; “If it is not red, then it is not my car.” Seeing “not red” implies “not my car.” Similarly, seeing that S is not a plausible outcome from P, tells you that H is not a plausible possibility. In such a situation, you can legitimately say, “I reject hypothesis H.”
Ironically, in the case of observing agreement between S and P, the only permissible statement is, “I fail to reject the hypothesis.” You certainly aren’t entitled to say that the evidence causes you to accept the hypothesis.
This is an emotionally unsatisfying situation. If your observations are consistent with your hypothesis, you certainly want to accept the hypothesis. But that is not an acceptable conclusion when performing a formal hypothesis test. There are only two permissible conclusions from a formal hypothesis test:
- I reject the hypothesis.
- I fail to reject the hypothesis.
In choosing a hypothesis to test, you need to keep in mind two criteria.
- Criterion 1: The more interesting outcome of a hypothesis test is “I reject the hypothesis.” So make sure to pick a hypothesis that it will be interesting to reject.
The role of this kind of hypothesis is to be refuted or nullified, so it is called the null hypothesis. We often denote the null hypothesis as \(H_0\).
What sorts of statements are interesting to reject? Often these take the form of the conventional wisdom or a claim of no effect. Rejecting such a claim suggests that there is an effect – and that’s interesting.
For example, in comparing two fever-reducing drugs, an appropriate null hypothesis is that the two drugs have the same effect. If you reject the null, you can say that they don’t have the same effect. But if you fail to reject the null, you’re in much the same position as before you started the study.
If we fail to reject the null, it may well be that null hypothesis is true, but it might simply be that our work was not adequate: not enough data, not a clever enough experiment, etc. Rejecting the null can reasonably be taken to indicate that the null hypothesis is false, but failing to reject the null tells you very little: many different hypotheses may all be consistent with the data at hand.
- Criterion 2: To perform the deductive stage of the test, you need to be able to calculate the distribution outcomes of the test statistic under the assumption that the null hypothesis is true. This means that the hypothesis needs to be specific.
The assumption that stock prices are a random walk has very definite consequences for how big a start-to-end change you can expect to see. On the other hand, the assumption “there is a trend” leaves open the question of what sort of trend it is and how big. It’s not specific enough to be able to figure out the consequences. We could test for a particular form of the trend, but if we reject such a hypothesis, all we are rejecting is that one specific form of the trend; there may be a different form of the trend.
13.4 The p-value
One of the consequences of randomness is that there isn’t a completely clean way to say whether the observations fail to match the consequences of the null hypothesis. In principle, this is a problem even with simple statements like “the car is red.” There is a continuous range of colors and at some point one needs to make a decision about how orange the car can be before it stops being red.
Figure 13.3 shows the probability distribution for the start-to-end stock price change under the null hypothesis that stock prices are a random walk. The observed value of the test statistic, $5446, falls under the tall part of the curve – it’s a plausible outcome of a random draw from the probability distribution.
The conventional way to measure the plausibility of an outcome is by a p-value . The p-value of an observation is always calculated with reference to a probability distribution derived from the null hypothesis.
P-values are closely related to percentiles. The observed value $5446 falls at the 81st percentile of the distribution. Being at the 81st percentile implies that 19 percent of draws would be even more extreme, falling even further to the right than $5446. So if the null hypothesis were true, we would observe a stock market change at least this big 19% of the time.
The p-value is the fraction of possible draws from the distribution that are as extreme or more extreme than the observed value. If the concern is only with values bigger than $5446, then the p-value is 0.19.
A small p-value indicates that the value of the test statistic computed from our sample would be quite surprising if the the null hypothesis is true. If the p-value is not small, then the value of test statistic computed from our sample is deemed plausible, even if the null hypothesis is true.
The convention in hypothesis testing is to consider the observation as being implausible when the p-value is less than 0.05. But note that
- 0.05 is just a convention,
- 0.05 is not the appropriate cut-off in all settings, and
- p-values are on a continuous scale – so p-values of 0.051 and 0.049 mean essentially the same thing, even though one of them is larger than 0.05 and the other is smaller.
In the stock market example, the p-value is larger than 0.05, so we fail to reject the null hypothesis that stock prices are a random walk with no trend. The random walk hypothesis and our data are plausibly consistent. (Of course, other hypotheses may also be consistent with the data.)
13.4.1 Statistical Significance
You will often see phrases like “statistically significant”, or “statistically significant at the \(\alpha = 0.5\) level”. All this means is that the associated hypothesis test had a p-value less than the threshold established for rejecting the null hypothesis.
For example, if a study finds a “statistically significant difference between to treatments”, that means they had a null hypothesis that there was no difference between the two treatments and obtained a small p-value (and probably the authors are equating small with “less than 0.05” unless they say something different).
It is always better to report the actual p-value rather than just reporting “significant” or “not significant” because the p-value conveys more information.
13.5 Hypothesis Testing as a 4-Step Process
The process of conducting a hypothesis test can be described as a 4-step process.
State the null hypothesis.
The null hypothesis is a statement about the population. More specifically, it is a statement about a parameter or parameters.
Compute a test statistic.
All the evidence in the data must be distilled down to a single number called the test statistic.
Determine the p-value.
The p-value is a probability: the probability of obtaining a test statistic at least as extreme (at least as unusual) and the one we observed, assuming that the null hypothesis is true.
To compute this probability, we need to determine the distribution the test statistic would have if we computed in from random samples drawn from a population where the null hypothesis is true. Sometimes there are theoretical methods that can tell us (at least approximately) what this distribution is. Another option is to simulate many data sets and compute the test statistic for each simulated sample.
Either way, we compare the test statistic computed from our actual data to this null distribuiton to determine the p-value.
Draw a conclusion.
A small p-value says that data like our data would be unusual if the null hypothesis were true. If the p-value is small enough, we will say that we reject the null hypothesis because our data are not very compatible with the hypothesis. In this case either:
- the null hypothesis is false, or
- the null hypothesis is true, but our data sets was unusual.
If the p-value is not small, then data similar to ours is plausibly consistent with the null hypothesis. This doesn’t mean the null hypothesis is true; the data may be consistent with many hypotheses, especially if the data set is small. In this case, we fail to reject the null hypothesis.
13.6 Type I error: Rejecting a true null hypothesis
The p-value for the hypothesis test of the possible trend in stock-price was 0.19, not small enough to justify rejecting the null hypothesis that stock prices are a random walk with no trend. A smaller p-value, one less than 0.05 by convention, would have led to rejection of the null. The small p-value would have indicated that the observed value of the test statistic would be unusual in a world where the null hypothesis is true.
Now turn this around. Suppose the null hypothesis really were true; suppose stock prices really are a random walk with no trend. In such a world, it’s still possible to see an implausible value of the test statistic. But, if the null hypothesis is true, then seeing an implausible value is misleading: it leads us to reject the null hypothesis even though the null hypothesis is actually true. This sort of mistake is called a Type I error.
Such mistakes are not uncommon. In a world where the null is true – the only sort of world where you can falsely reject the null – if we use the conventional threshold of 0.05, then type I errors will happen for 5% of samples.
The way to avoid such mistakes is to lower the p-value threshold for rejecting the null. Lowering it to, say, 0.01, would make it harder to mistakenly reject the null. On the other hand, it would also make it harder to correctly reject the null in a world where the null ought to be rejected.
The threshold value of the p-value below which the null should be rejected is a probability: the probability of rejecting the null in a world where the null hypothesis is true. This probability is called the significance level of the test.
It’s important to remember that the significance level is a conditional probability. It is the probability of rejecting the null in a world where the null hypothesis is actually true. Of course that’s a hypothetical world, not necessarily the real world.
13.7 Alternative Hypotheses
In the stock-price example, the large p-value of 0.19 led to a failure to reject the null hypothesis that stock prices are a random walk. Such a failure doesn’t mean that the null hypothesis is true, although it’s encouraging news to people who want to believe that the null hypothesis is true.
You never get to “accept the null” because there are reasons why, even if the null were wrong, we might not get a small p-value.
- You might have been unlucky. The randomness of the sample might have obscured your being able to see the trend in stock prices.
- You might not have had enough data. Perhaps the trend is small and can’t easily be seen.
- Your test statistic might not be sensitive to the ways in which the system differs from the null hypothesis. For instance, suppose that there is an small average tendency for each day’s activity on the stock market to undo the previous day’s change: the walk isn’t exactly random. Looking for large values of the start-to-end price difference will not reveal this violation of the null. A more sensitive test statistic would be the correlation between price changes on successive days.
13.7.1 Type II error: failing to reject when the null hypothesis is false
It can be helpful to think about another hypothesis in addition to the null hypothesis – an alternative hypothesis. This is another hypothesis about the world that differs from the null hypothesis – something that might be true if the null hypothesis is incorrect. In the hypothesis-testing drama, an alternative hypothesis plays a relatively small role since the only possible outcomes of a hypothesis test are (1) reject the null and (2) fail to reject the null. So the alternative hypothesis is not directly addressed by the outcome of a hypothesis test.
The main roles of the alternative hypothesis are
- to guide you in interpreting the results if you do fail to reject the null;
- to help you decide how much data to collect.
To illustrate, suppose that the stock market really does have a trend hidden inside the random day-to-day fluctuations with a standard deviation of $106.70. Imagine that the trend is $2 per day: an alternative hypothesis to the null hypothesis that there is no trend.
Suppose the world really were like this alternative hypothesis. In this world the null hypothesis is false, but we still might not reject it based on our sample data. Failing to reject the null hypothesis even though some alternative is in fact true is called Type II error. The probability of making a type II error depends on both the null hypothesis (from which we compute the p-value) and the alternative hypothesis (from which we generate data).
In our stock market example, a type II error would occur if there really is a trend of $2 per day, but our sample data doesn’t lead us to reject the null hypothesis. We could simulate 10 years worth of data assuming the alternative $2 per day trend many times to find out how often such data sets don’t allow us to reject the null hypothesis (because the p-value isn’t small enough).
This logic can be confusing at first. It’s tempting to reason that, if the alternative hypothesis is true, then the null must be false. So how could you fail to reject the null? And, if the alternative hypothesis is assumed to be true, why would you even consider the null hypothesis in the first place? But keep in mind that neither the null hypothesis nor the alternative hypothesis should be taken as “true.” They are just competing hypotheses, conjectures used to answer “what-if?” questions: What could happen if the null hypothesis were true? What could happen if some alternative were true? Furthermore, each hypothesis is consistent with a variety of data sets (and test statistics). For some data sets, both hypotheses may be plausible – the data aren’t sufficient to rule one of them out.
13.7.2 Power
The flipside of type II error is power: If the alternative hypothesis is true, how likely are we to reject the null hypothesis (a desirable result since the null hypothesis would be false in this case). The probability of rejecting the null hypothesis when the alternative is true is called power.
Here are the steps in calculating the power of the hypothesis test of stock market prices. The null hypothesis is that prices are a pure random walk as illustrated in Figure 13.2. The alternative hypothesis is that in addition to the random component, the stock prices have a systematic trend of increasing by $2 per day.
Go back to the null hypothesis world and determine which test statistics that would cause you to reject the null hypothesis. This is called the rejection region of the test. It is the same for any alternative – it only depends on the null hypothesis and our p-value threshold for rejecting it.
Referring to Figure \(\ref{fig:stock-hist}\), you can see that a test statistic of $11,000 or greater would have produced a p-value of 0.05.
Now return to the alternative hypothesis world. In this world, what is the probability that the test statistic would have been bigger than $11,000? This question can be answered by the same sort of simulation as in Figure \(\ref{fig:stocks-random}\) but with a $2 price increase added each day. Doing the calculation gives a probability of \(0.16\).
Power is the probability of rejecting the null hypothesis in a world where the alternative is true. Of course, if the alternative hypothesis is true, then the null hypothesis is false, so it’s completely appropriate to reject the null, so a large power is desirable. 16% is pretty small for power. Even if there really is a trend of $2 per day, we only have a 16% chance of rejecting the null hypothesis of no trend, using this test with this much data. In other words, the study is quite weak. Even if this alternative is correct, we only have a 16% chance that it will produce data sufficient to reject the hypothesis that there is no trend at all.
How can we increase the power of our study? Here are some possibilities:
Use more data (a larger sample).
Generally, as the sample size increases, power increases.
Use a more powerful test.
The choice of test statistic matters. Sometimes a better test statistic can lead to more power.
Use a more extreme alternative hypothesis.
The more different the world of the alternative hypothesis is from the world of the null hypothesis, the more likely data generated in the world of the alternative hypothesis will be to cause us to reject the null hypothesis. This is just another way of saying that it is easier to detect large departures from the null hypothesis than smaller ones. There is more power to detect a trend of $4 per day than a trend of $2 per day.
But we can’t choose the alternative just to get larger power. The alternative needs to be plausible and interesting. Having large power against an implausible alternative doesn’t say much about the usefulness of our study. Often power is cacluated for several different alternives to see how power depends on the particular alternative.
Of the three options above, the first is the easiest one for the modeler to adjust. A modeler should, of course, always be using reasonably powerful tests that are appropriate for the given situation, and power analysis can be used to help decide which of several approaches to use. Adjusting the alternative simply to increase the number calculated as power is not a legitimate practice. Increasing the sample size, however, is appropriate and nearly always increases power.
But in most cases larger samples cost more. It takes more time and resources to conduct more surveys or run more laboratory tests. Fortunately, it is usually feasible to figure out in advance how large the study should be to achieve reasonable power. This is the primary use of power calculations – to select a reasonable sample size for the goals of a study. There is little reason to conduct a study with power that is too low since we are not likely to learn anything useful. There is also little reason to spend extra resources on a study that is more powerful than necessary since beyond a certain amount of power, incremental gains in power require large increases in the sample size – a smaller data set would be much more cost effective and have nearly as much power. Typically, researchers aim to have power around 80 or 90% if they can.
In our stock market example, it turns out that reliably detecting – with power of 80%, say – a $2 per day trend in stock prices requires about 75 years worth of data. This long historical period is probably not relevant to today’s investor. Indeed, it’s nearly all the data that is actually available: the DJIA was started in 1928.
When the power is small for realistic amounts of data and realistic alternative hypotheses, the phenomenon you are seeking to find may be undetectable. In that case, it may be better to spend resources investigating something else.
13.8 A Glossary of Hypothesis Testing
Null Hypothesis: A statement about the world that you are interested to disprove (to nullify).
The null hypothesis is almost always something that is clearly relevant and not controversial: that the conventional wisdom is true or that there is no relationship between variables.
Examples:
- “The drug has no influence on blood pressure.”
- “Smaller classes do not improve school performance.”
- “Women and men are equally likely to repond to a particular advertising campaign by placing an order.”
There are only two allowed outcomes of a hypothesis test and both relate only to the null hypothesis:
- Reject the null hypothesis.
- Fail to reject the null hypothesis.
Alternative Hypothesis: A statement about the world that motivates your study and stands in contrast to the null hypothesis.
Examples:
- “The drug will reduce blood pressure by 5 mmHg on average.”
- “Decreasing class size from 30 to 25 will improve test scores by 3%.”
- “Women are twice as likely as men to repond to a particular advertising campaign by placing an order.”
The outcome of the hypothesis test is not informative about the alternative. The importance of the alternative is in setting up the study: choosing a relevant test statistic and collecting enough data.
Test Statistic: The number that you use to summarize your the data in a study.
This might be the sample mean, a model coefficient, or some other number. Later chapters will give several examples of test statistics that are particularly appropriate for modeling.
Type I Error: The error of rejecting a null hypothesis when it is actually true. Type I errors can only be made if the null hypothesis is true.
Type II Error: The error of not rejecting a null hypothesis even though it is false. Type II errors can only be made if the null hypothesis is false.
p-value: This is the usual way of presenting the result of the hypothesis test. It is a probability that quantifies how atypical the observed value of the test statistic would be in a world where the null hypothesis is true.
NoteIn reports, p-values should generally be reported with 1 or 2 significant digits. More digits than that are not meaningful. (But note: software often reports many additional digits that you won’t want to include in your report.)
Significance Level: The largest p-value that will cause us to reject the null hypothesis. Often denoted \(\alpha\).
Traditionally, in many disciplines hypothesis tests are set up so that the significance level will is 0.05 (1 in 20). But it is always better to report the p-value than to simply report whether it is above or below the significance level. This allows anyone to interpret the results with any significance level they desire and avoids making big distinctions based on small differences in p-value near the significance level.
The primary use for significance levels is in determining power.
Statistically Significant: We say a result is statistically significant if the corresponding hypothesis test produced a p-value small enough to cause us to reject the null hypothesis. If a fixed significance level has been chosen, this means that the p-value is smaller than the signficance level \(\alpha\).
Importantly, the statistically significant does not mean important or substantial. It only means that the effect is discrenable in our data. In large samples, even very small (and unimportant) effects can be statistically significant. And in small samples, it is possible that important effects may go undetected.
On remedy for this potential confusion is to also look at a confidence interval for the quantity being investigated. That will give us an sense for how large the effect is and how precisely we know it.
Power: The probability of rejecting the null hypothesis assuming a particular alternative hypothesis is true.
Larger power is generally better – within reason. The costs associated with increasing power beyond 95% are generally not worth the gains. When designing studies, researchers often aim to have power between 80% and 90% for some alternative that is both interesting and plausible. But this is not nearly as standardized as the use of a significance level of \(\alpha = 0.05\).
Power calculations can be a bit complicated. It is more important at this point to understand the concept of power than to be able to perform power calculations.
null and alternative: Common casual abbreviations for the null hypothesis and the alternative hypothesis.
Often you will hear people talk about “rejecting the null” or “computing power against the alternative” with out explicitly saying the word hypothesis.
13.9 Update on Stock Prices
Figure 13.1 shows stock prices over the 10-year period from Dec. 5, 1997 to Nov. 14, 2007. For comparison, Figure Figure 13.4 shows a wider time period, the 25-year period from 1985 to the month this section is being written in 2011.
When the first edition of this book was being written, in 2007, the 10-year period was a natural sounding interval, but a bit more information on the choice can help to illuminate a potential problem with hypothesis testing. I wanted to include a stock-price example because there is such a strong disconnection between the theories of stock prices espoused by professional economists – daily changes are a random walk – and the stories presented in the news, which wrongly provide a specific daily cause for each small change and see “bulls” and “bears” behind month- and year-long trends. I originally planned a time frame of 5 years – a nice round number. But the graph of stock prices from late 2002 to late 2007 shows a pretty steady upward trend, something that’s visually inconsistent with the random-walk null hypothesis. I therefore changed my plan, and included 10-years worth of data. If I had waited another year, through the 2008 stock market crash, the upward trend would have been eliminated. In 2010 and early 2011, the market climbed up again, only to fall dramatically in mid-summer.
That change from 5 to 10 years was inconsistent with the logic of hypothesis testing. I was, in effect, changing my data – by selecting the start and end points – to make them more consistent with the claim I wanted to make. This is always a strong temptation, and one that ought to be resisted or, at least, honestly accounted for.
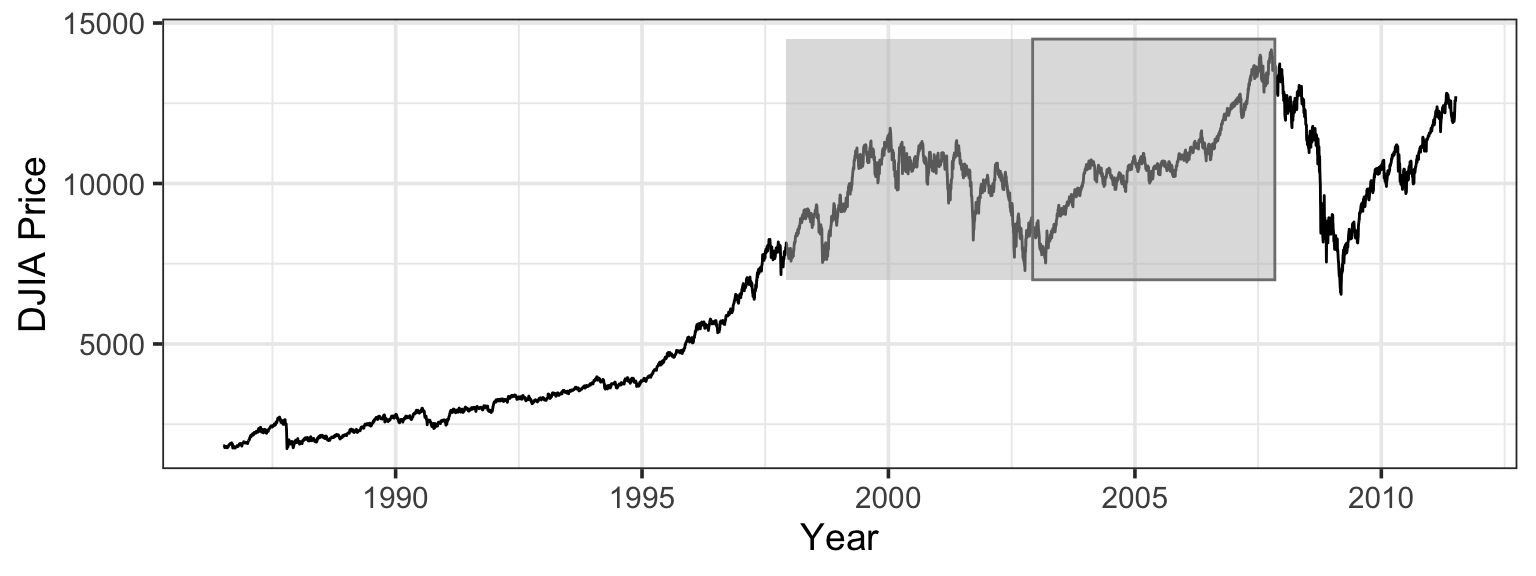
The selection of data that make one’s case appear especially strong is sometimes referred to as cherry picking1 and is considered an unethical data practice. Cherry picking can be intentional (with an attempt to deceive or inflate one’s evidence) or unintentional (through oversight or carelessness).
Although it is possible to adjust for this, most people engaged in cherry picking do not make the necessary adjustments. As an example, if we choose the data set by selecting the 5-year interval within the last 50 years that shows the largest gains, then p-value calculations should be based on simulations of 50 years worth of data and the largest 5-year gain within that interval. By definition, this will be a larger gain than we would see if we only simulated 5 years, so it would lead to a larger p-value than the p-value based on simulating only 5 years worth of data.
In principle, it is best if the analysis methods are completely specified before any data is analyzed, or even collected. That helps avoid the temptation to cherry pick the data or the analysis method to get the preferred outcome. In practice, it is often the case that modeling decisions continue to be made after the data are in hand. It is important that this is clearly indicated in reports and that appropriate adjustments are made to the analyses when this is warranted.
The term comes from an analogy to picking only the best cherries from a tree, which would lead to misleading representation of the overall quality of the cherries produced by the tree.↩︎