6 Language of Models
I do not believe in things. I believe only in their relationships. – Georges Braque (1882-1963) cubist painter
Mathematicians do not study objects, but relations among objects. – Henri Poincarè (1854-1912) mathematician
Chapter 4 is concerned with model forms based on division into groups. Those models are very common, but their utility is limited: the models can be misleading because they fail to take into account multiple factors that can shape outcomes, not just simple membership in a group. This chapter starts down the path toward more sophisticated models. The point of departure will be a set of concepts and a notation for describing models that are more general and therefore more flexible than simple groupwise models.
One October I received a bill from the utility company: $56 for natural gas for the month. According to the bill, the average outdoor temperature during October was 56°F (9.5°C).
I had particular interest in this bill because two months earlier, in August, I replaced the old furnace in our house with a new, expensive, high-efficiency furnace that’s supposed to be saving gas and money. This bill was the first one of the heating season, and I wanted to know whether the new furnace was working.
To be able to answer such questions, I kept track of my monthly utility bills. The gasbill variable shows a lot of variation: from $3.42 to $240.9 per month. The 50% coverage interval is $23.42 to $124.18. The mean bill is $81.24. Judging from this, the $56 October bill is low. It looks like the new furnace is working!
But perhaps that conclusion is premature. My new furnace is just one factor that can influence the gas bill. Some others: the weather, the price of natural gas (which fluctuates strongly from season to season and year to year), the thermostat setting, whether there were windows or doors left open, how much gas we use for cooking, etc. Of all the factors, I think the weather and the price of natural gas are the most important. I’d like to take these into account when judging whether the $56 bill is high or low.
Rather than looking at the bill in dollars, it makes sense to look at the quantity of gas used. After all, the new furnace can only reduce the amount of gas used, it doesn’t influence the price of gas. According to the utility bill, the usage in October was 32 ccf. (“ccf” means cubic feet, one way to measure the quantity of gas.) The variable ccf gives the historical values from past bills: the range is 0 to 242 ccf, so 32 ccf seems pretty good – it’s lower than the median monthly usage, which is 60 ccf. Still, this doesn’t take into account the weather.
Now it is time to build a model: a representation of the utility data for the purpose of telling whether 32 ccf is low or high given the temperature. The variable temperature contains the average temperature during the billing period.
A simple graph of ccf versus temperature will suffice. (See Figure 6.1.) The solid point shows the October bill (56° and 32 ccf). The gray line indicates which points to look at for comparison, those from months near 56°.
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.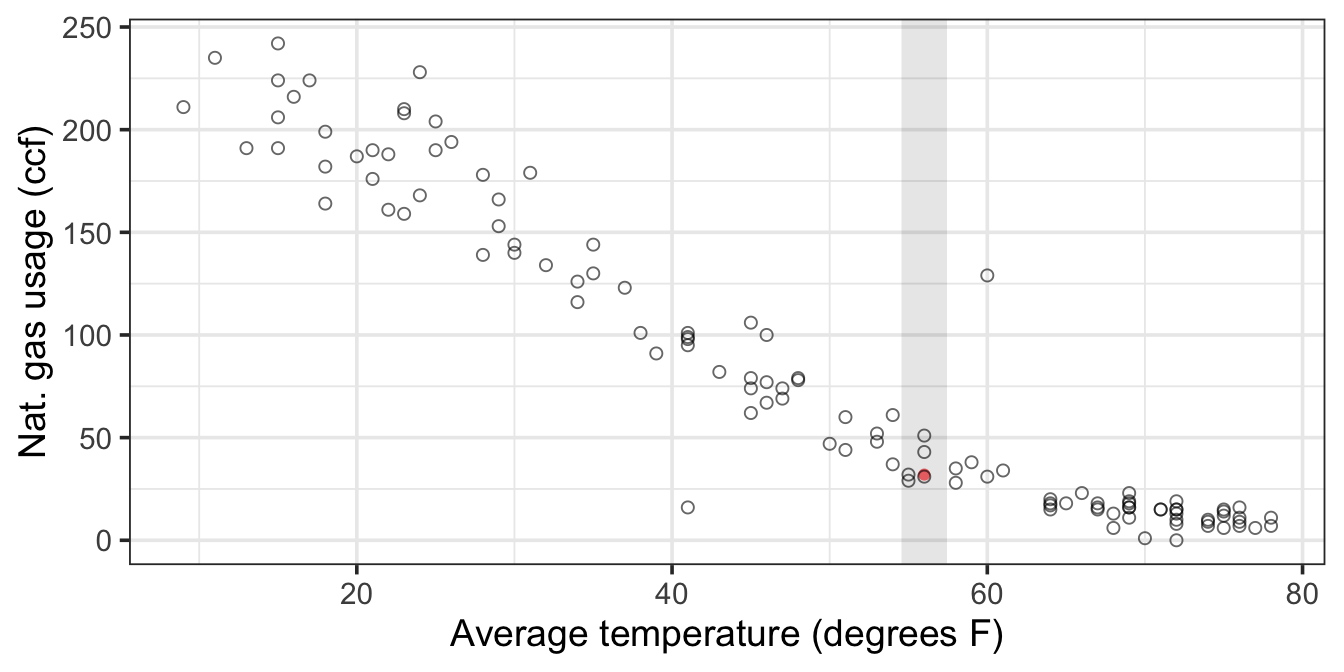
The graph suggests that 32 ccf is more or less what to expect for a month where the average temperature is 56°. The new furnace doesn’t seem to make much of a difference.
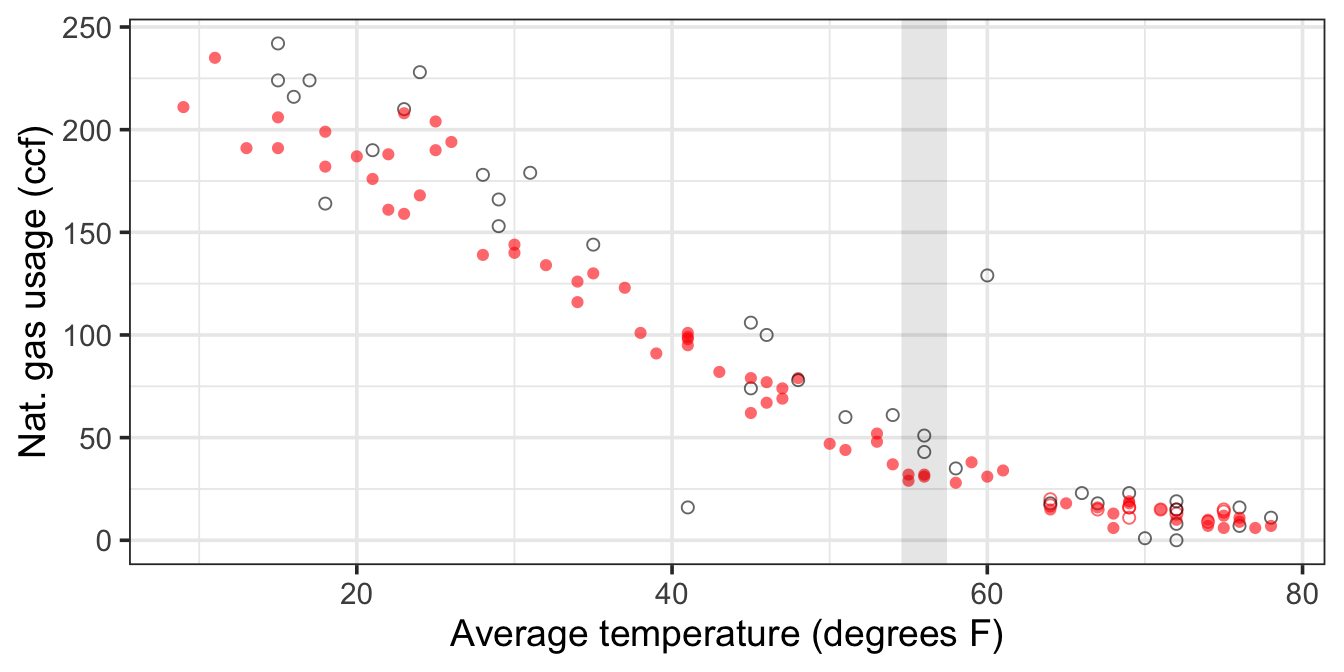
Here is a slightly more nuanced way to look at things. It wasn’t available immediately after installing the furnace, but after several more years of gas bills, we can compare the bills with and without the new furnace at a range of temperatures. Let’s remake the plot in Figure 6.1 using the plot symbol to show which months were with the old furnace (open) and with the new furnace (open). Looking at Figure 6.2, we can see that the solid dots are perhaps slightly lower than the open dots (at least for temperatures below 60 degrees). So perhaps the new furnace is making a modest difference.
6.1 Models as Functions
Figure 6.1 and Figure 6.2 give a pretty good idea of the relationship between gas usage and temperature (and presence of a new furnace).
The concept of a function is very important when thinking about relationships. A function is a mathematical concept: it describes the relationship between an output and one or more inputs. One way to talk about a function is that you plug in the inputs and receive back the output. For example, the formula \(y = 3x + 7\) can be read as a function with input \(x\) and output \(y\). Plug in a value of \(x\) and receive the output \(y\). So, when \(x\) is 5, the output \(y\) is 22.
One way to represent a function is with a formula, but there are other ways as well, for example graphs and tables. Figure 6.3 shows a function representing the relationship between gas usage and temperature. The function is much simpler than the data. In the data, there is a scatter of usage levels at each temperature. But in the function there is only one output value for each input value.
`geom_smooth()` using method = 'loess'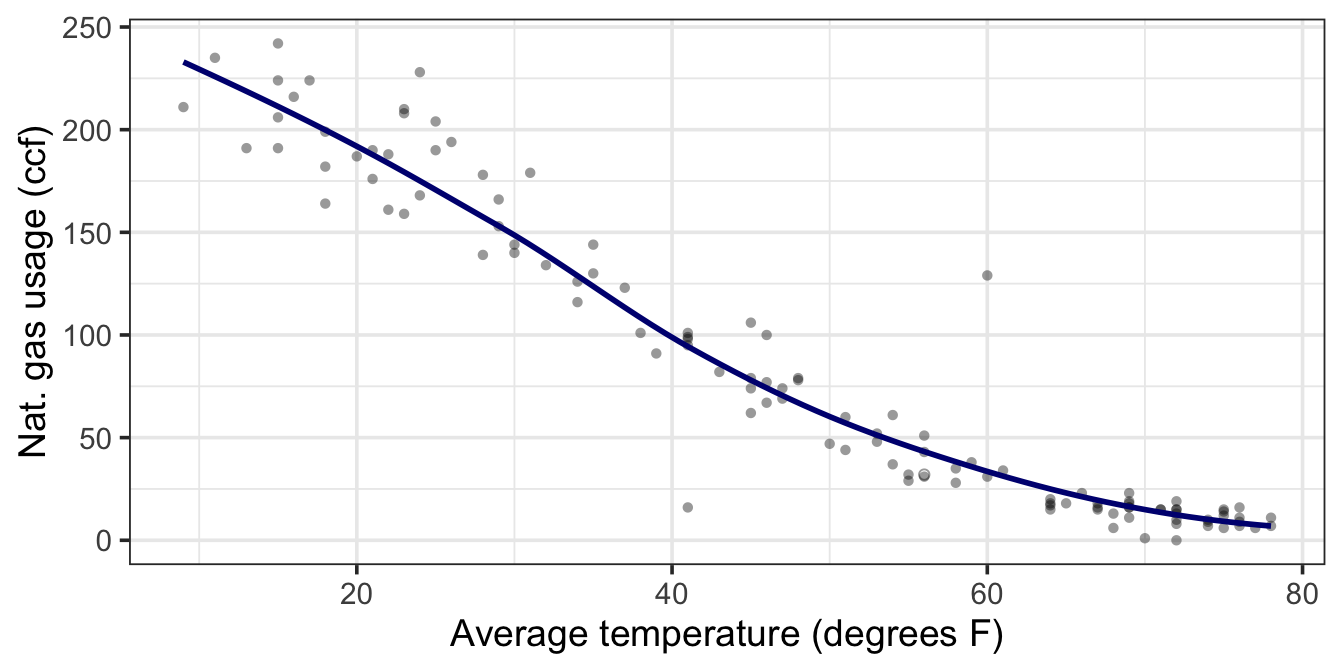
Some vocabulary will help to describe how to represent relationships with functions.
The response variable is the variable whose behavior or variation you are trying to understand. On a graph, the response variable is conventionally plotted on the vertical axis.
The explanatory variables are the other variables that you want to use to explain the variation in the response. Figure 6.1 shows just one explanatory variable,
temperature. It’s plotted on the horizontal axis. It’s plotted on the horizontal axis. Figure 6.2 shows an example with two explanatory variables, adding whether the furnace is new or old totemperatureand using color to show it on the plot.Conditioning on explanatory variables means taking the value of the explanatory variables into account when looking at the response variables. When in Figure 6.1 you looked at the gas usage for those months with a temperature near 56°, you were conditioning gas usage on temperature.
The model value is the output of a function. The function – called the model function – has been arranged to take the explanatory variables as inputs and return as output a typical value of the response variable. That is, the model function gives the typical value of the response variable conditioning on the explanatory variables. The function shown in Figure 6.3 is a model function. It gives the typical value of gas usage conditioned on the
temperature. For instance, at 56°, the typical usage is 32 ccf. At 20°, the typical usage is much higher, about 200 ccf.For every case in the data set, its residual is how far the observed response value is above or below the corresponding model value. For example, one of the cases plotted in Figure 6.3 is a month where the
temperaturewas 13° and the gas usage was 191 ccf. When the input is 13°, the model function gives an output of 228 ccf. So, for that case, the residual is 191 - 228 = -37 ccf. Remember:\[ \mbox{residual} = \mbox{actual value} - \mbox{model value} \]
Graphically, the residual for each case tells how far above the model function that case is. A negative residual means that the case is below the model function.
The idea of a function is fundamental to understanding statistical models. Whether the function is represented by a formula or a graph or a computer algorithm, the function takes one or more inputs and produces an output. In the statistical models in this book, that output is the model value, a “typical” or “ideal” value of the response variable at given levels of the inputs. The inputs are values of the explanatory variables.
The model function describes how the typical value of the response variable depends on the explanatory variables. The output of the model function varies along with the explanatory variables. For instance, when temperature is low, the model value of gas usage is high. When temperature is high, the model value of gas usage is low. The idea of “depends on” is very important. In some fields such as economics, the term dependent variable is used instead of “response variable.” Other phrases are used for this notion of “depends on,” so you may hear statements such as these: “the value of the response given the explanatory variables,” or “the value of the response conditioned on the explanatory variables.”
The model function describes a relationship. If you plug in values for the explanatory variables for a given case, you get the model value for that case. The model value is usually different from one case to another, at least so long as the values of the explanatory variables are different. When two cases have exactly the same values of the explanatory values, they will have exactly the same model value even though the actual response value might be different for the two cases.
The residuals tell how each case differs from its model value. Both the model values and the residuals are important. The model values tell what the model thinks is typical or average for a given set of explanatory variable values. The residuals tell how far from typical an individual case is. Taken together, the distribution of the residuals tell us something about how from the the model value individual cases are likely to be – even cases that are not in the data set.
As already said, models partition the variation in the response variable. Some of the variability is explained by the model, the remainder is unexplained. The model values capture the “deterministic” or “explained” part of the variability of the response variable from case to case. The residuals represent the “random” or “unexplained” part of the variability of the response variable.
Keep in mind that our model functions will typically have more than one input because our models will have more than one explanatory variable. Most situations are too complicated to sufficiently explain with only two variables.
6.2 Model Functions with Multiple Explanatory Variables
This section presents two examples of models with more than one explanatory variable.
6.2.1 Home heating example
Figure 6.4 shows an example of a model with two explanatory variables – temperature and furnace. To read the plot we need to use the temperature (\(x\)-axis) and furnace (color) to read off the typical natural gas usage. As the number of explanatory variables increases, representing models graphically becomes more challenging, but computing outputs from inputs is not fundamentally harder.

In this case, the furnace appears to be making only a modest difference.
6.2.2 Wages
Historically, women tended to be paid less than men. To some extent, this reflected the division of jobs along sex lines and limited range of jobs that were open to women – secretarial, nursing, school teaching, etc. But often there was simple discrimination; an attitude that women’s work wasn’t as valuable or that women shouldn’t be in the workplace, or that men had to provide for a family. Over the past thirty or forty years, the situation has changed. Training and jobs that were once rarely available to women – police work, management, medicine, law, science – are now open to them.
Surveys consistently show that women still tend to earn less than men: a “wage gap.” To illustrate, consider data from one such survey, the Current Population Survey (CPS) from 1985. CPS In the survey data, each case is one person. The variables are the person’s hourly wages at the time of the survey, age, sex, marital status, the sector of the economy in which they work, etc.
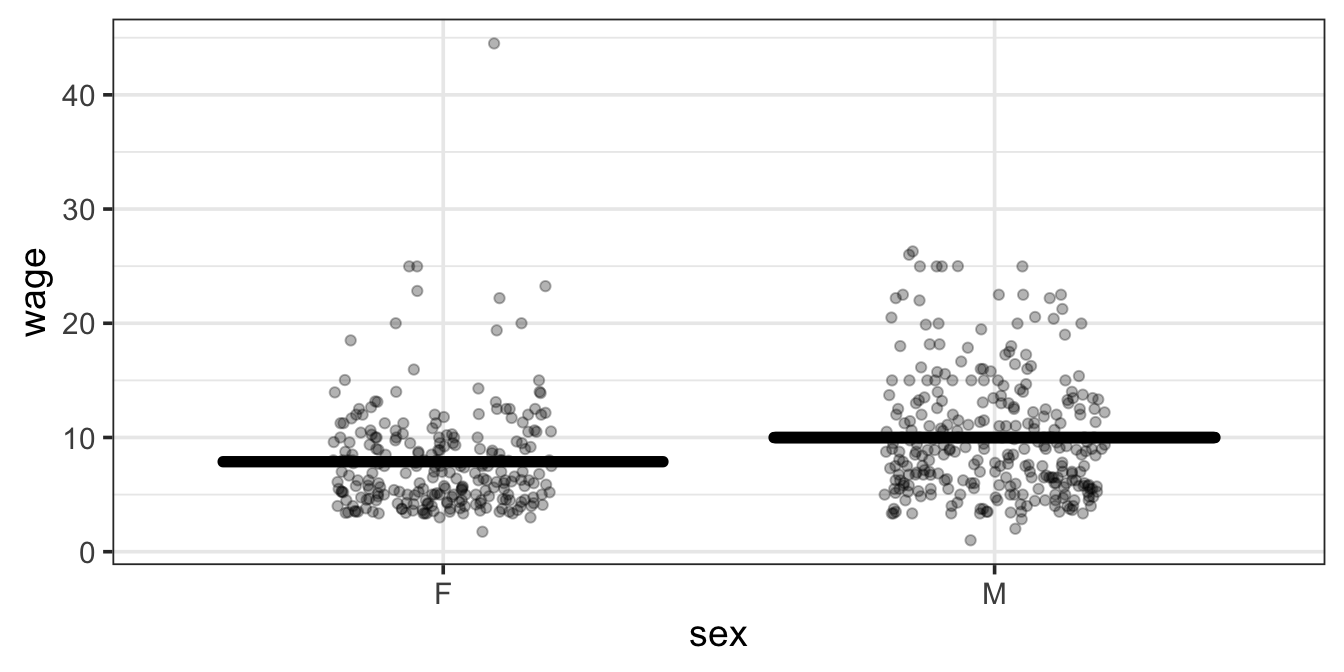
One aspect of these data is displayed by plotting wage versus sex, as in Figure 6.5. The model plotted along with the data show that typical wages for men are higher than for women.
The situation is somewhat complex since the workforce reflected in the 1985 data is a mixture of people who were raised in the older system and those who were emerging in a more modern system. A woman’s situation can depend strongly on when she was born. This is reflected in the data by the age variable.
There are other factors as well. The roles and burdens of women in family life remain much more traditional than their roles in the economy. Perhaps marital status ought to be taken into account. In fact, there are all sorts of variables that you might want to include – job type, race, location, etc.
A statistical model can include multiple explanatory variables, all at once. To illustrate, consider explaining wage using the worker’s age, sex, and marital status.
In a typical graph of data, the vertical axis stands for the response variable and the horizontal axis for the explanatory variable. But what do you do when there is more than one explanatory variable? One approach, when some of the explanatory variables are categorical, is to use differing symbols or colors to represent the differing levels of the categories. Figure 6.6 and Figure 6.7 show wages versus age, sex, and marital status plotted out this way.
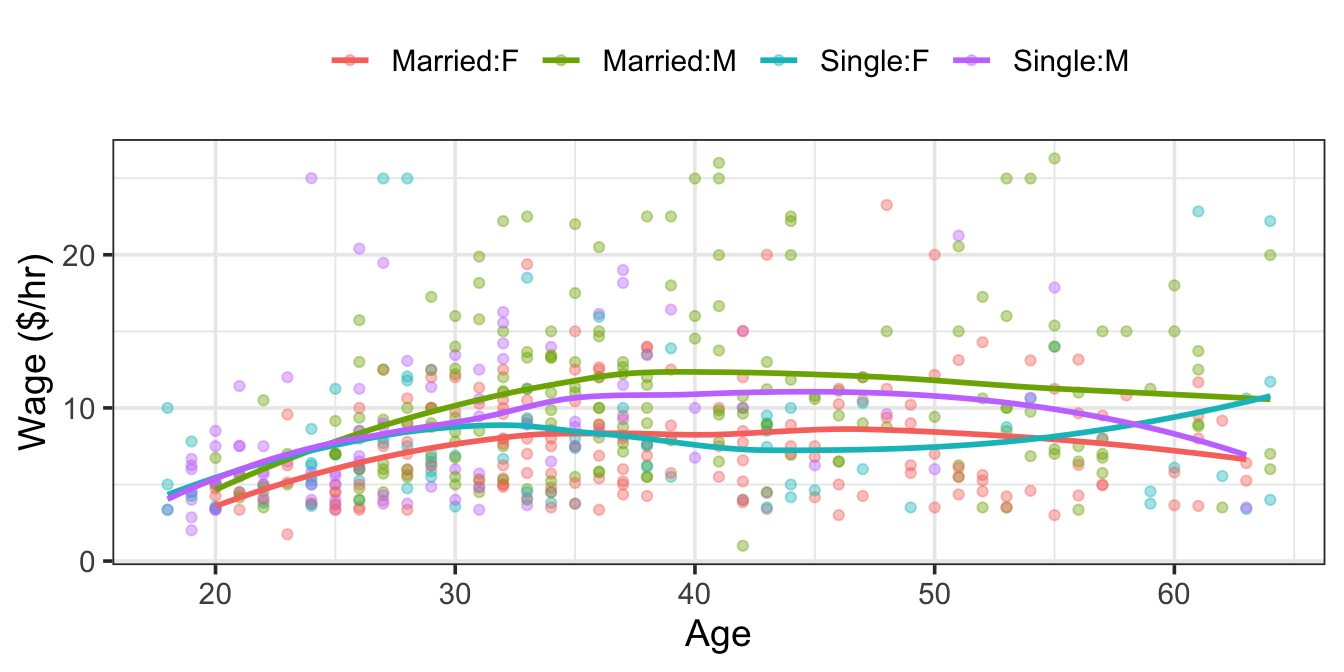
The first thing that might be evident from the scatter plot is that not very much is obvious from the data on their own. There does seem to be a slight increase in wages with age, but the cases are scattered all over the place.
The model, shown as the continuous curves in Figure 6.6, simplifies things. The relationships shown in the model are much clearer. You can see that wages tend to increase with age, up until about age 40, and they do so differently for men and for women and differently for married people and single people.
Models can sometimes reveal patterns that are not evident in a graph of the data. This is a great advantage of modeling over simple visual inspection of data. There is a real risk, however, that a model is imposing structure that is not really there on the scatter of data, just as people imagine animal shapes in the stars. The model shown in Figure 6.6 is not the only model that could be used with these data. Figure 6.7 shows another model. This model forces the relationship between wages and age to be linear – it isn’t possible for wages to rise and then fall as they appear to do in Figure 6.6.
Warning: Using the `size` aesthietic with geom_line was deprecated in ggplot2 3.4.0.
ℹ Please use the `linewidth` aesthetic instead.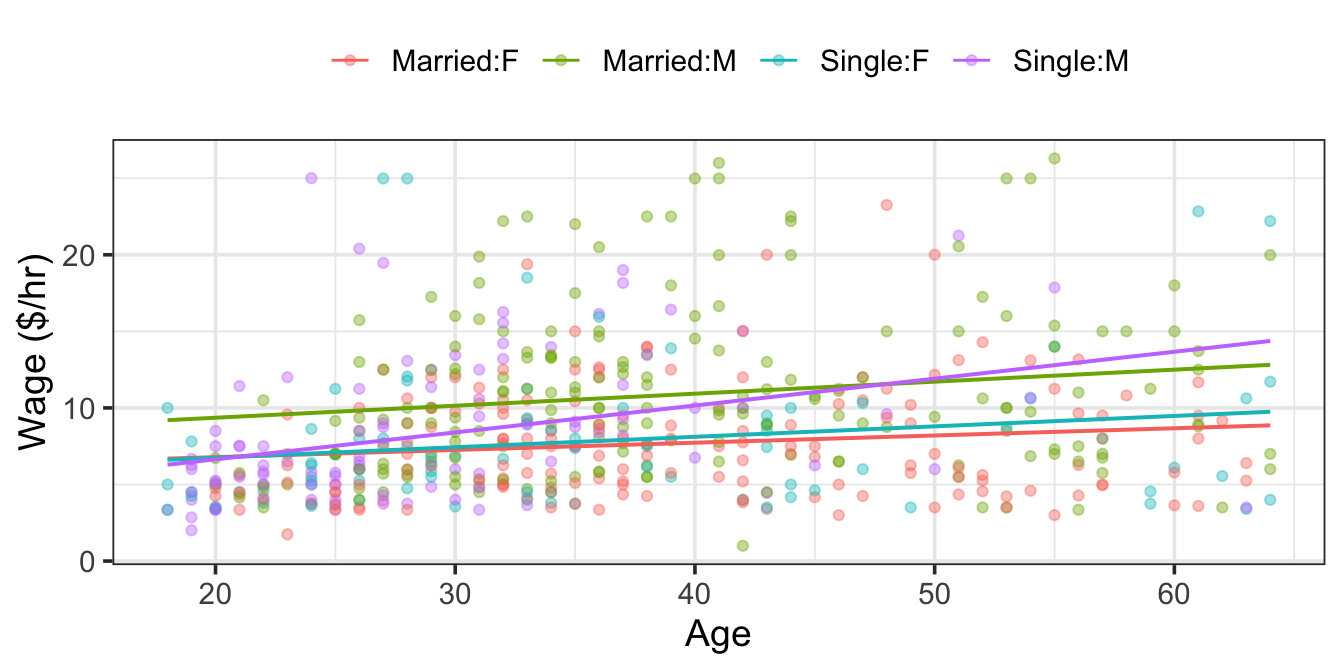
So which model is correct? Is either model correct? That isn’t really the right question. It has famously been said that all models are wrong, but some models are useful. So we really want to know whether a model is useful, not whether it is “correct.” A skeptical approach is always warranted. Much of the second half of the book is about ways to judge whether the structure suggested by a model is justified by the data.
There is a tendency for those who first encounter models to fix attention on the clarity of the model and ignore the variation around the model. This is a mistake. Keep in mind the definition of statistics offered in the first chapter:
Statistics is the explanation of variation in the context of what remains unexplained.
The scatter of the wage data around the model is very large; this is a very important part of the story. The scatter suggests that there might be other factors that account for large parts of person-to-person variability in wages, or perhaps just that randomness plays a big role.
Compare the broad scatter of wages to the rather tight way the gas usage in Figure 6.1 is modeled by average temperature. The wage model is explaining only a small part of the variation in wages, the gas-usage model explains a much larger part of the variation in those data.
Adding more explanatory variables to a model can sometimes usefully reduce the size of the scatter around the model. If you included the worker’s level of education, job classification, age, or years working in their present occupation, the unexplained scatter might be reduced. Even when there is a good explanation for the scatter, if the explanatory variables behind this explanation are not included in the model, the scatter due to them will appear as unexplained variation. (In the gas-usage data, it’s likely that wind velocity, electricity usage that supplements gas-generated heat, and the amount of gas used for cooking and hot water would explain a lot of the scatter. But these potential explanatory variables were not measured.)
6.3 Reading a Model
There are two distinct ways that you can read a model.
Read out a model value. Plug in specific values for the explanatory variables and read out the resulting model value. For the model in Figure 6.1, an input temperature of 35° produces a predicted output gas usage of 125 ccf. For the model in Figure 6.6 a single, 30-year old female has a model value of $8.10 per hour. (Remember, the model is based on data from 1985!)
Describe the relationship expressed by the model. In contrast to reading out a model value for some specific values of the explanatory variables, here interest is in the overall relationship: how gas usage depends on temperature; how wages depend on sex or marital status or age.
Reading out the model value is useful when you want to make a prediction (What would the gas usage be if the temperature were 10° degrees?) or when you want to compare the actual value of the response variable to what the model says is a typical value. (Is the gas usage lower than expected in the 56° month, perhaps due to my new furnace?).
Characterizing the relationship is useful when you want to make statements about broad patterns that go beyond individual cases. Is there really a connection between marital status and wage? Which way does it go? The “shape” of the model function tells you about such broad relationships. Reading the shape from a graph of the model is not difficult.
6.3.1 Slope
For a quantitative explanatory variable, e.g., temperature or age, the model form is a continuous curve or line. An extremely important aspect of this curve is its slope. For the model of gas usage in Figure 6.3, the slope is down to the right: a negative slope. This means that as temperature increases, the gas usage goes down. In contrast, for the model of wages in Figure 6.7, the slope is up to the right: a positive slope. This means that as age increases, the wage goes up.
The slope is measured in the usual way: rise over run.
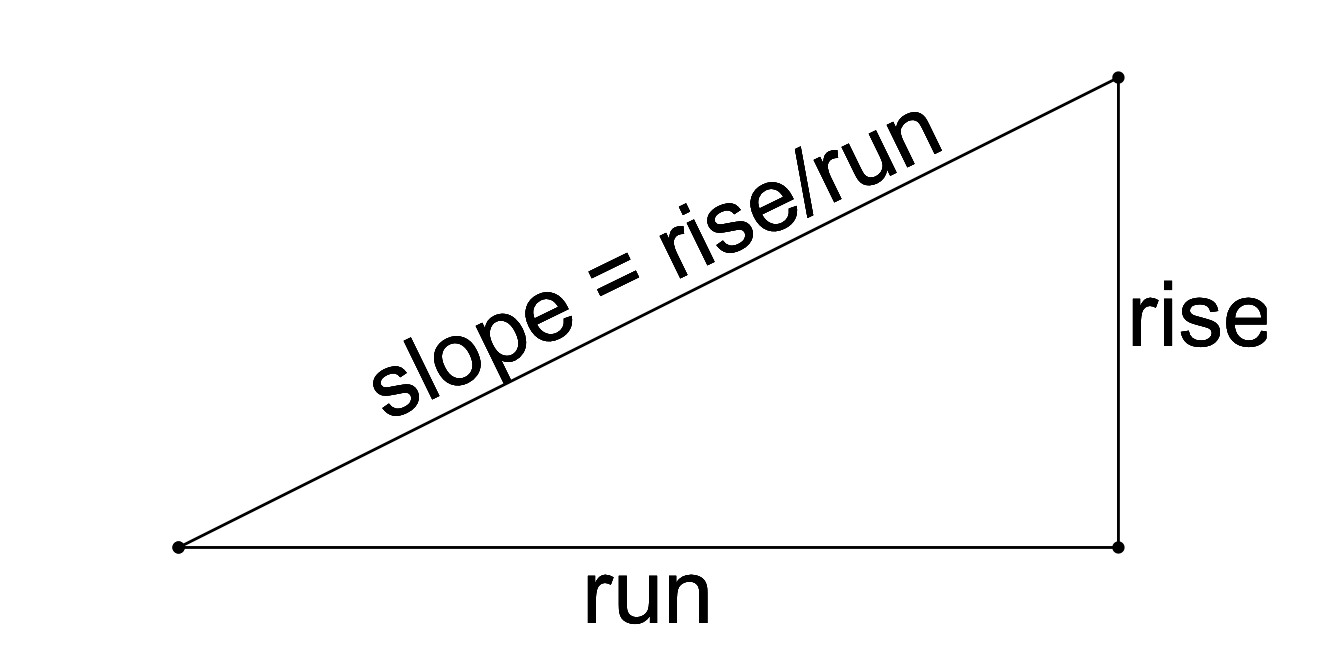
For a straight line, we can compute the rise and run from any two points on the line. (Note that rise can be negative if the line “falls” rather than “rises”.) We will get the same slope every time. For a curve, we use the “slope of the tangent line” – the slope of a line that is “moving in the same direction as the curve” at that point. We can estimate the slope of the tangent line using the slope of the secant line – the line connecting two points on the curve that are close together. Many of our models will include coefficients that measure the slope of a line or a curve the represents the model function.
The numerical size of the slope in a model tells us about the relationship between the response varaible and and explanatory variable. The sign tells which way the relationship goes. Some examples:
For the gas usage model in Figure 6.3 in winter-like temperatures, the slope is about -4 ccf/degree. This means that gas usage can be expected to go down by 4 ccf for every degree of temperature increase.
For the model of wages in Figure 6.7, the slope for single females is about 0.20 dollars-per-hour/year: for every year older a single female is, wages typically go up by 20 cents-per-hour.
Slopes have units. These are always the units of the response variable divided by the units of the explanatory variable. In the wage model, the response has units of dollars-per-hour while the explanatory variable age has units of years. Thus the units of the slope are dollars-per-hour/year.
For categorical variables, slopes don’t apply in quite the same way. Instead of having a line or a curve, we have a “dotted line” with no values between the dots. The slope of the line connecting these dots measures how much the model value changes as we move from category to category. It can be useful to think of this as a difference rather than as a slope:
- In the model where wage is explained only by sex, the difference between typical wages for males and females is 2.12 dollars per hour.
When there is more than one explanatory variable, there will be a distinct slope or difference associated with each.
6.3.2 Models can’t tell cause from association
When describing models, the words used can carry implications that go beyond what is justified by the model itself. Saying “the difference between typical wages” is pretty neutral: a description of the pattern. But consider this statement: “Typical wages go up by 20 cents per hour for every year of age.” There’s an implication here of causation, that as a person ages his or her wage will go up. That might in fact be true, but the data on which the model is based were not collected in a way to support that claim. Those data don’t trace people as they age; they are not longitudinal data. Instead, the data are a snapshot of different people at different ages: cross-sectional data.
It’s dangerous to draw conclusions about changes over time from cross-sectional data of the sort in the CPS data set. Perhaps people’s wages stay the same over time but that the people who were hired a long time ago tended to start at higher wages than the people who have just been hired.
Consider this statement: “A man’s wage rises when he gets married.” The model in Figure 6.6 is consistent with this statement; it shows that a married man’s typical wage is higher than an unmarried man’s typical wage. But does marriage cause a higher wage? It’s possible that this is true, but that conclusion isn’t justified from the data. There are other possible explanations for the link between marital status and wage. Perhaps the men who earn higher wages are more attractive candidates for marriage. It might not be that marriage causes higher wages but that higher wages cause marriage.
To draw compelling conclusions about causation, it’s important to collect data in an appropriate way. For instance, if you are interested in the effect of marriage on wages, you might want to collect data from individuals both before and after marriage and compare their change in wages to that over the same time period in individuals who don’t marry. As described in Chapter 19, the strongest evidence for causation involves something more: that the condition be imposed experimentally, picking the people who are to get married at random. Such an experiment is hardly possible when it comes to marriage.
6.4 Choices in Model Design
The suitability of a model for its intended purpose depends on choices that the modeler makes. There are three fundamental choices:
- The data.
- The response variable.
- The explanatory variables.
6.4.1 The Data
How were the data collected? Are they a random sample from a relevant sampling frame? Are they part of an experiment in which the values of one or more variables were determined (usually randomly) as part of the design of the study, or are they observational data? Are the relevant variables being measured? (This includes those that may not be directly of interest but which have a strong influence on the response.) Are the variables being measured in a meaningful way?
If you are conducting a statistical anlysis yourself, start thinking about your models and the variables you will want to include while you are still planning your data collection. You want to be sure you have collected the right data for the model you will eventually use to analyse the situation.
When you are confronted with a situation where your data are not suitable, or not as ideal as you would like, then you need to be realistic and honest about the limitations of the conclusions you can draw from the data you have. Some of the issues involved will be discussed starting in Chapter 18.
6.4.2 The Response Variable
The appropriate choice of a response variable for a model is often obvious. The response variable should be the thing that you want to predict, or the thing whose variability you want to understand. Often the response is something that you think is the effect produced by some cause. But the relationship need not be causal, and models can be used to predict causes from effects as well as to predict effects from causes.
For example, in examining the relationship between gas usage and outdoor temperature, it seems clear that gas usage should be the response: temperature is a major determinant of gas usage. But suppose that the modeler wanted to be able to estimate outdoor temperature from the amount of gas used. Then it would make sense to take temperature as the response variable and gas usage as the explanatory variable.
Similarly, wages make sense as a response variable when you are interested in how wages vary from person to person depending on traits such as age, experience, and so on. But suppose that a sociologist was interested in assessing the influence of income on personal choices such as marriage. Then the marital status might be a suitable response variable, and wage would be an explanatory variable.
Most of the modeling techniques in this book require that the response variable be quantitative. The main reason is that there are straightforward ways to measure variation in a quantitative variable and measuring variation is key to assessing the reliability of models. There are, however, methods for building models with a categorical response variable. (One of them, logistic regression, is the subject of Chapter 17)
6.4.3 Explanatory Variables
Much of the thought in modeling goes into the selection of explanatory variables and later chapters in this book describes several ways to decide if an explanatory variable ought to be included in a model.
Of course, some of the things that shape the choice of explanatory variables are obvious. Do you want to study sex-related differences in wage? Then sex had better be an explanatory variable. Is temperature a major determinant of the usage of natural gas? Then it makes sense to include temperature as an explanatory variable.
You will see situations where including an explanatory variable hurts the model, so it is important to be careful. (This will be discussed in Chapter 12.) A much more common mistake is to leave out important explanatory variables. Unfortunately, few people learn the techniques for handling multiple explanatory variables and so your task will often need to go beyond modeling to include explaining how this is done. When designing a model, you should think hard about potential explanatory variables and be prepared to include them in a model along with the variables that are of direct interest.
6.5 Model Terms
Once the modeler has selected explanatory variables, a choice must be made about how to include them in the model.
Consider the three examples in Figure 6.9. Notice that the various models have graphs of different shapes. The gas-usage model is a gentle curve, the wage-vs-sex model is just two values – one for men and one for women, and the more elaborate wage model is four lines with different slopes and intercepts.
`geom_smooth()` using method = 'loess'
The modeler determines the shape of the model through his or her choice of model terms. The basic idea of a model term is that explanatory variables can be included in a model in more than one way. Each kind of term describes a different way to include a variable in the model.
You need to learn to describe models using model terms for several reasons. First, you will communicate in this language with the computers that you will use to perform the calculations for models. Second, when there is more than one explanatory variable, it’s hard to visualize the model function with a graph. Knowing the language of model terms will help you “see” the shape of the function even when you can’t graph it. Third, model terms are the way to talk about “parts” of models. In evaluating a model, statistical methods can be used to take the model apart and describe the contribution of each part. This analysis – the word “analysis” literally means to loosen apart – helps the modeler to decide which parts are worth keeping.
There are just a few basic kinds of models terms. They will be introduced by example in the following sections
- intercept term: a sort of “baseline” that is included in almost every model.
- main terms: the effect of explanatory variables directly.
- interaction terms how different explanatory variables modulate the relationship of each other to the response variable.
- transformation terms: simple modifications of explanatory variables.
Models almost always include the intercept term and a main term for each of the explanatory variables. Transformation and interaction terms can be added to create more expressive or flexible shapes, but many useful models do not include these.
To form an understanding of how different kinds of terms contribute to the overall “shape” of the model function, it’s best to look at the differently shaped functions that result from including different model terms. The next section illustrates this. Several differently shaped models are constructed of the same data plotted in Figure 6.10. The data are the record time (in seconds) for the 100-meter freestyle race along with the year in which the record was set and the sex of the swimmer. The response variable will be time, the explanatory variables will be year and sex.
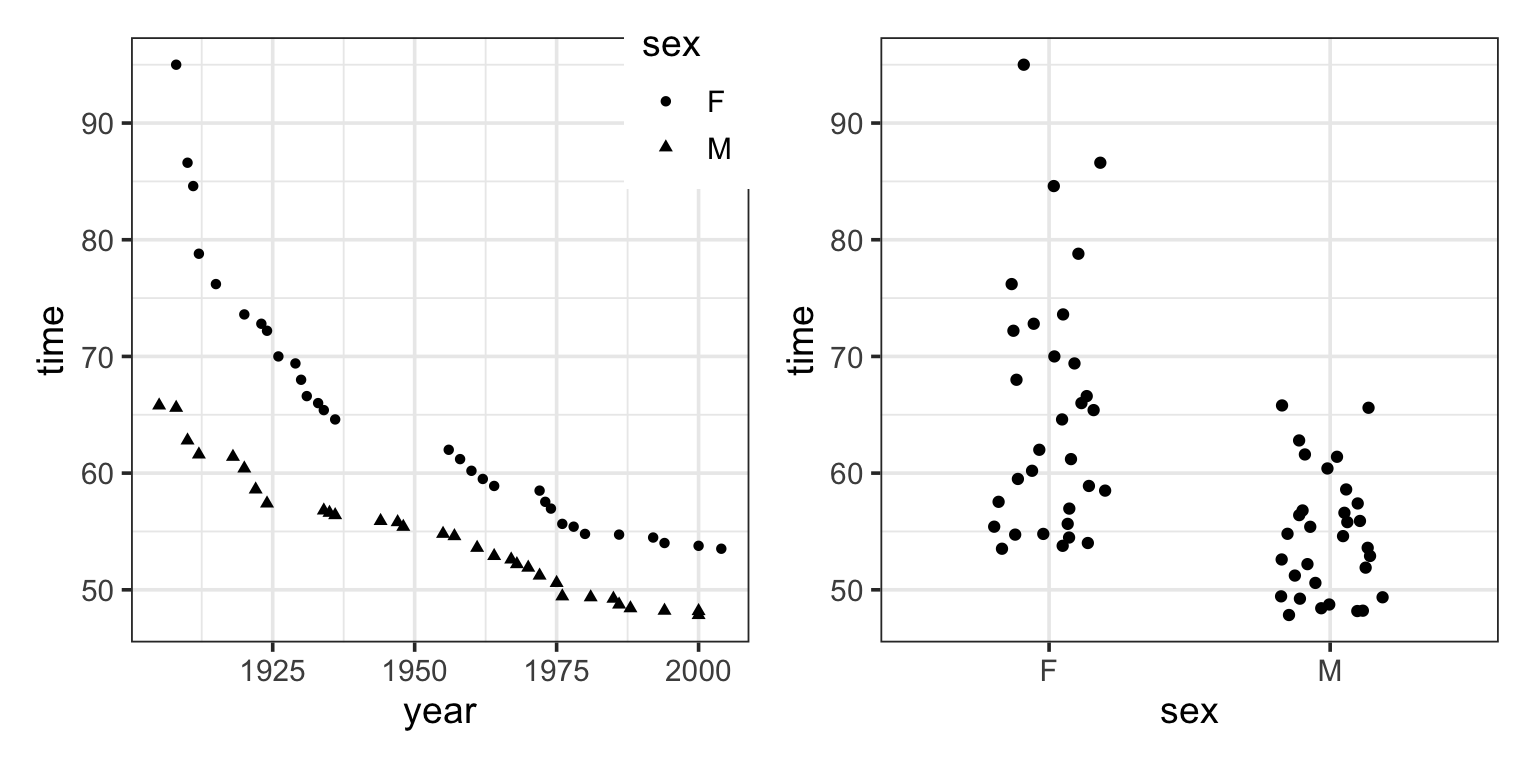
Figure 6.10 shows some obvious patterns, seen most clearly in the plot of time versus year. The record time has been going down over the years. This is natural, since setting a new record means beating the time of the previous record. There’s also a clear difference between the men’s and women’s records; men’s record times are faster than women’s, although the difference has decreased markedly over the years.
The following models may or may not reflect these patterns, depending on which model terms are included.
6.5.1 The Intercept Term (and no other terms)
The intercept term is included in most statistical models. The intercept term is a bit strange because it isn’t something you measure; it isn’t a variable, it’s just a number. The term “intercept” will make more sense when model formulas are introduced in the next chapter.
Figure 6.11 shows the swimming data with a simple model consisting only of the intercept term: every model value is the same number – the intercept.
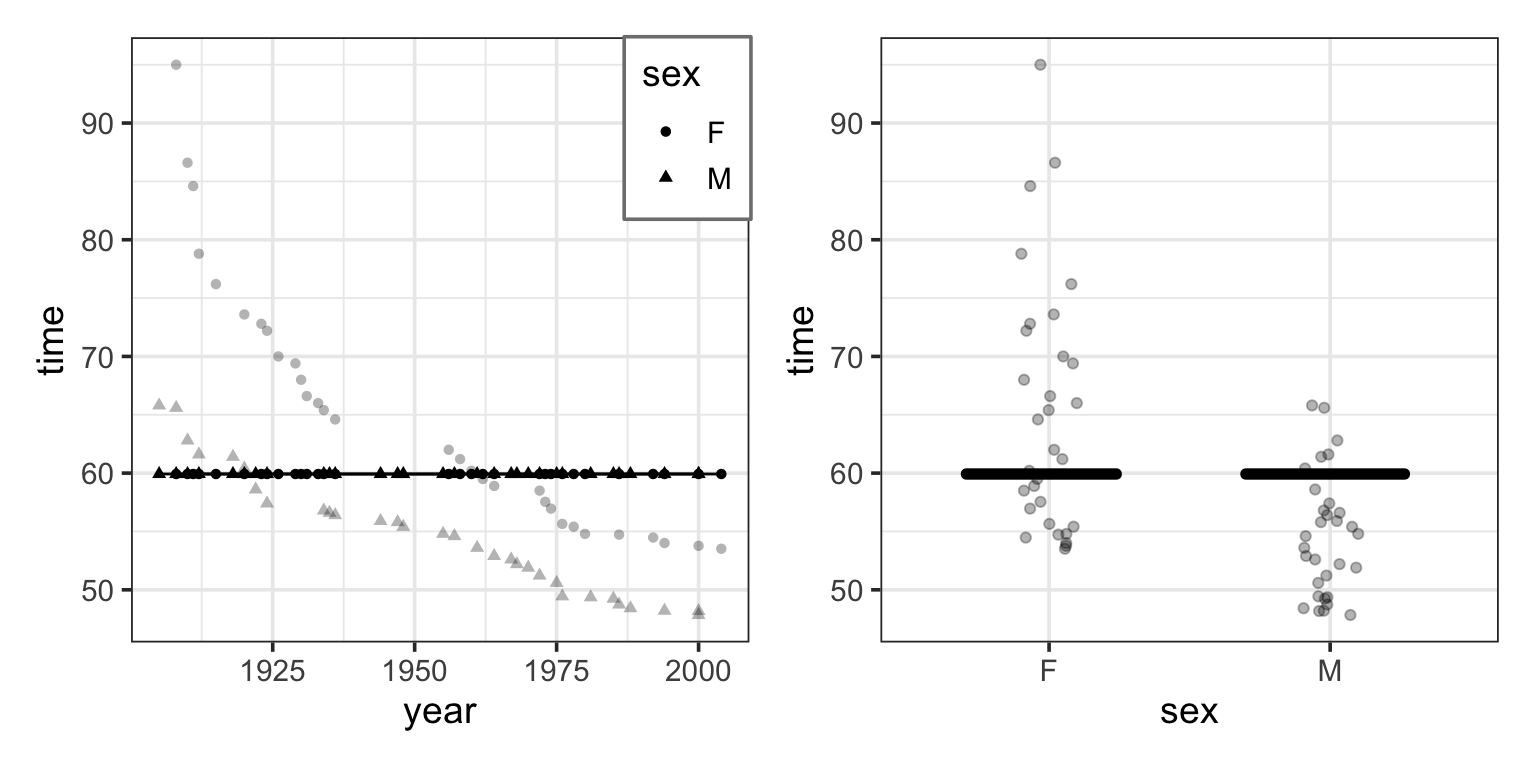
The model value for this model is exactly the same for every case. In order to create model variation from case to case, you would need to include at least one explanatory variable in the model.
6.5.2 Intercept and Main Terms
The most basic and common way to include an explanatory variable is as a main effect. Almost all models include the intercept term and a main term for each of the explanatory variables. The figures below show three different models each of this form:
The intercept and a main term from year
This model produces model values that vary with year, but show no difference between the sexes. This is because sex has not been included in the model.
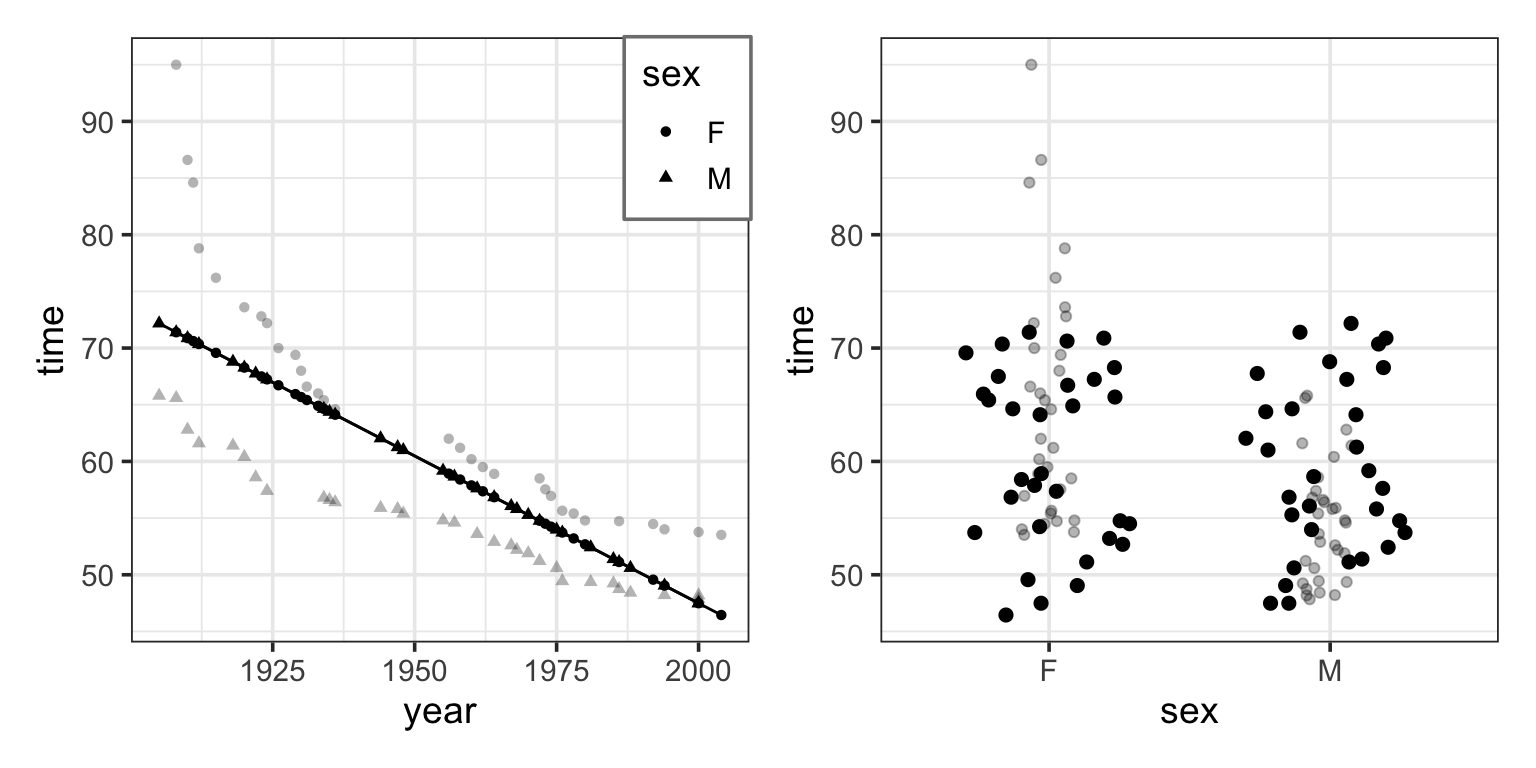
The model values have been plotted out as small black dots. The model pattern is evident in the left graph: swim time versus year. But in the right graph – swim time versus sex – it seems to be all scrambled. Don’t be confused by this. The right-hand graph doesn’t include year as a variable, so the dependence of the model values on year is not at all evident from that graph. Still, each of the model value dots in the left graph occurs in the right graph at exactly the same vertical coordinate.
The intercept and a main term from sex
This model produces different model values for each level of sex.

There is no model variation with year because year has not been included in the model.
The intercept and main terms from sex and from year
This model gives dependence on both sex and year.
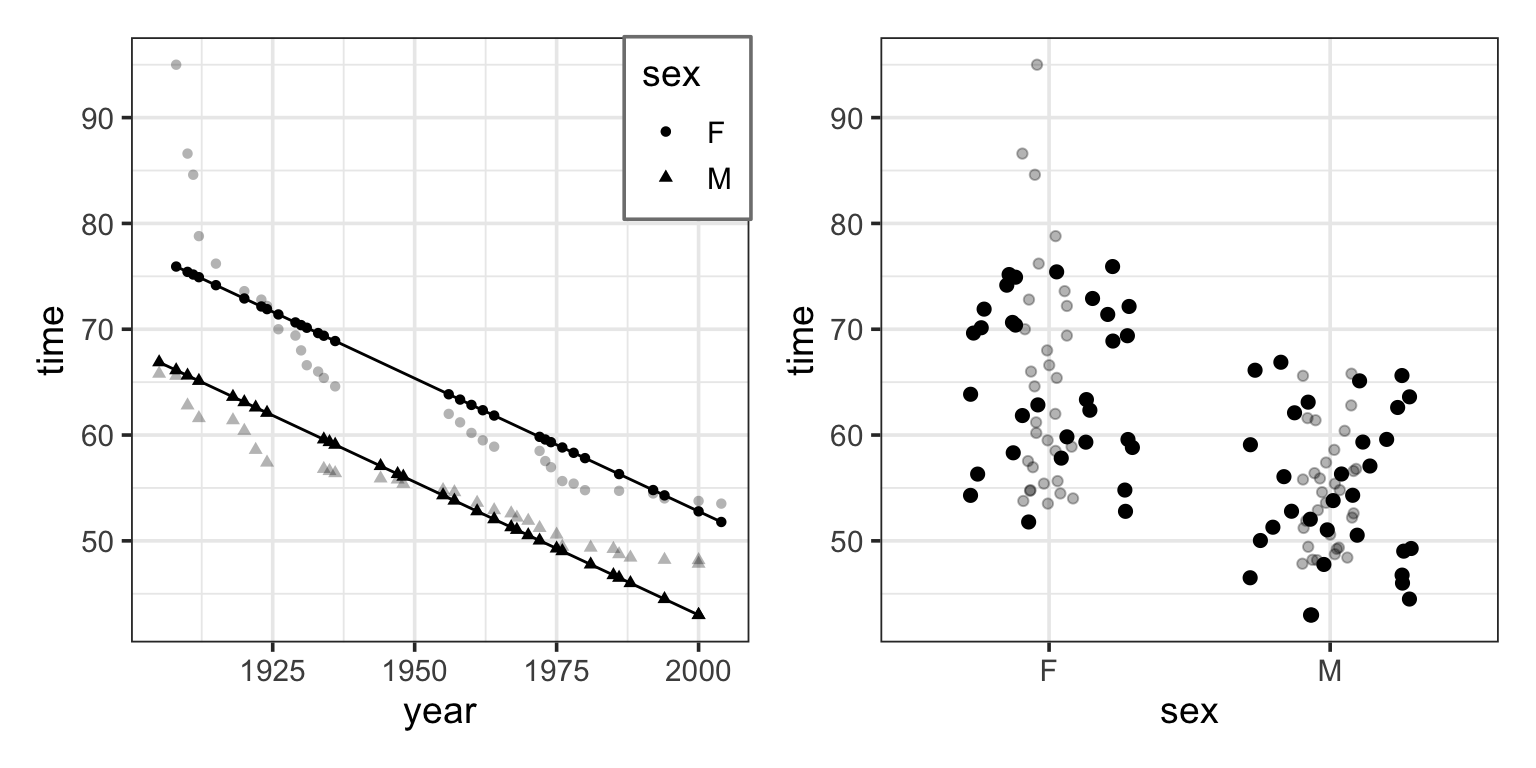
Note that the model values form two parallel lines in the graph of time versus year: one line for each sex.
6.5.3 Interaction Terms
Interaction terms combine two other terms, typically two main terms. An interaction term can describe how one explanatory variable modulates the role of another explanatory variable in modeling the relationship of both with the response variable.
In the graph, including the interaction term between sex and year produces a model with two non-parallel lines for time versus year. (The model also has the main terms for both sex and year and the intercept term, as always.)

One way to think about the meaning of the interaction term in this model is that it describes how the effect of sex changes with year. Looking at the model, you can see how the difference between the sexes changes over the years; the difference is getting smaller. Without the interaction term, the model values would be two parallel lines; the difference between the lines wouldn’t be able to change over the years.
Another, equivalent way to put things is that the interaction term describes how the effect of year changes with sex. The effect of year on the response is reflected by the slope of the model line. Looking at the model, you can see that the slope is different depending on sex: steeper for women than men.
For most people, it’s surprising that one term – the interaction between sex and year – can describe both how the effect of year is modulated by sex, and how the effect of sex is modulated by year. But these are just two ways of looking at the same thing.
A common misconception about interaction terms is that they describe how one explanatory variable affects another explanatory variable. Don’t fall into this error. Model terms are always about how the response variable depends on the explanatory variables, not how explanatory variables depend on one another. An interaction term between two variables describes how two explanatory variables combine jointly to influence the response variable.
Once people learn about interaction terms, they are tempted to include them everywhere. After all, it’s natural to think that world record swimming times would depend differently on year for women than for men. Of course wages might depend differently on age for men and women! Regretably, the uncritical use of interaction terms can lead to poor models. The problem is not the logic of interaction, the problem is in the data. Interaction terms can introduce a problem called multi-collinearity which can reduce the reliability of models. (See Chapter 12.) Fortunately, it’s not hard to detect multi-collinearity and to drop interaction terms if they are causing a problem. The model diagnostics that will be introduced in later chapters will make it possible to play safely with interaction terms.
6.5.4 Transformation Terms
A transformation term is a modification of another term using some mathematical transformation. Transformation terms only apply to quantitative variables. Some common transformations are \(x^2\) or \(\sqrt{x}\) or \(\log(x)\), where the quantitative explanatory variable is \(x\).
A transformation term allows the model to have a dependence on \(x\) that is not a straight line. The graph shows a model that includes these terms: an intercept, main effects of sex and year, an interaction between sex and year, and a year-squared transformation term.
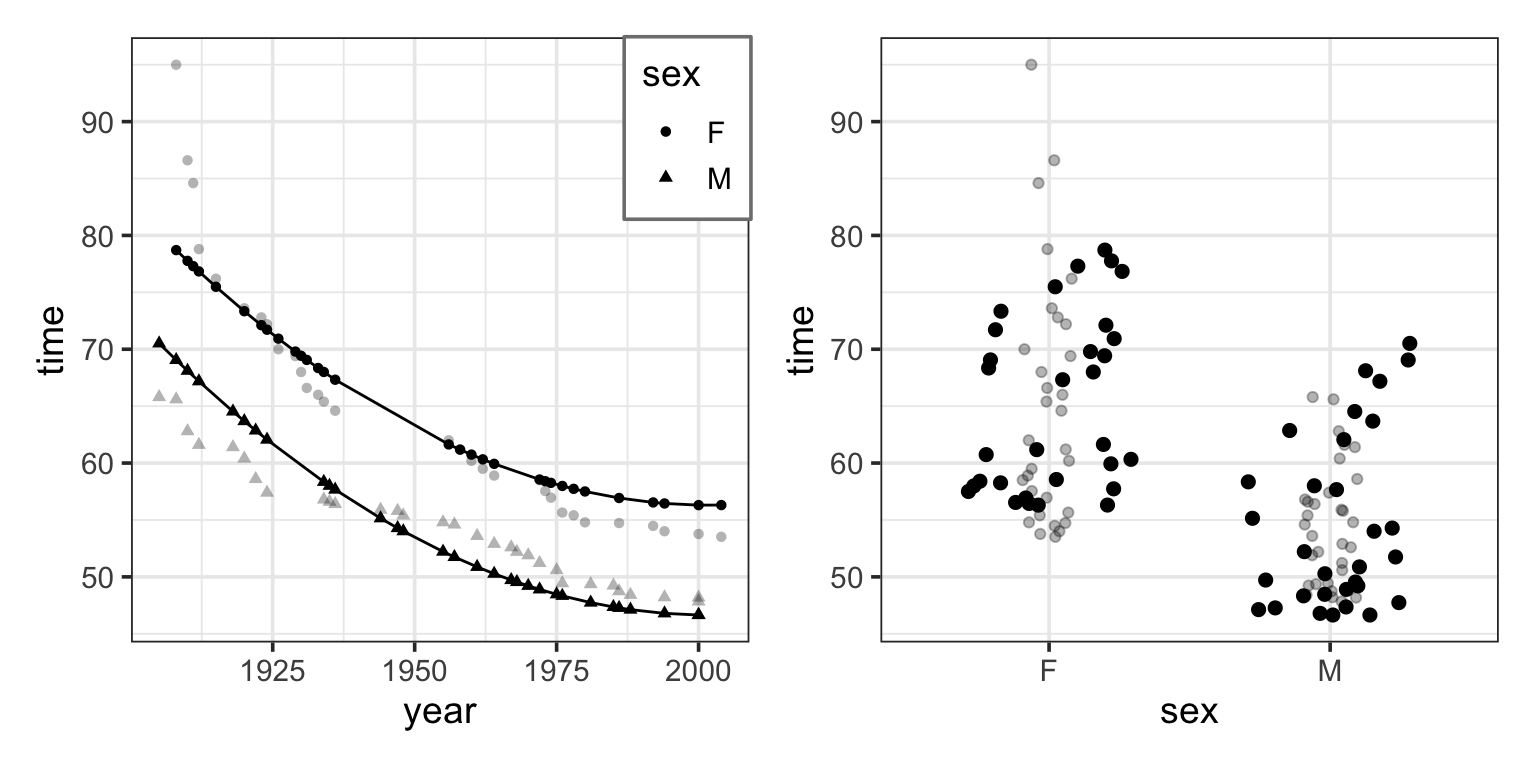
Adding in the year-squared term provides some curvature to the model function.
6.5.5 Aside: Are swimmers slowing down?
Look carefully at the model with a year-squared transformation term. You may notice that, according to the model, world record times for men have been getting worse since about year 1990. This is, of course, nonsense. Records can’t get worse. A new record is set only when an old record is beaten.
But the quadratic model doesn’t know this common sense about records – the model terms allow the model to curve in a certain way (a parabola) and the model curves in exactly that way. All parabolas rise to a peak and then fall or fall to a valley and then rise. If your knowledge of the data doesn’t agree with that shape, be careful about including quadratic terms in the model. Things may work out fine if the peak or valley happens to be far from the region of interest, but there is no guarantee that the nodel will behave at all sensibly – all it knows to do is fit a parabola.
What you probably want out of a model of world records is a slight curve that’s constrained never to slope upward. That’s doable, but not with the simple sorts of models we are describing.
Indeed, it is an unresolved problem in statistics how best to include in a model additional knowledge that you might have such as “world records can’t get worse with time.”
Even though models constructed with intercepts, main terms, interaction terms, and transformation terms cannot do everything, they are amazingly flexible. And if you get to know these ingredients well and then find that they are not sufficient for a particular application, you will be able to learn other types of models later, building on this foundation.

6.5.6 Main Effects without the Intercept
It’s possible to construct a model with main terms but no intercept terms. If the explanatory variables are all quantitative, this is almost always a mistake. Figure 6.18, which plots the model function for swim time modeled by age with no intercept term, shows why.

The model function is sloping slightly upward rather than falling as the data clearly indicate. This is because, without an intercept term, the model value is forced to be 0 when year is 0. This, of course, makes no sense for record swim times. The line must slope up from there to get near the data. It’s no wonder that the model function fails to look anything like the data.
Never leave out the intercept unless you have a very good reason. Indeed, statistical software typically includes the intercept term by default. You have to go out of your way to tell the software to exclude the intercept.
6.6 Notation for Describing Model Design
There is a concise notation for specifying the choices made in a model design, that is, which is the response variable, what are the explanatory variables, and what model terms to use. This notation, introduced originally in (Chambers and Hastie 1992), will be used throughout the rest of this book and you will use it in working with computers.

To illustrate, here is the notation for some of the models looked at earlier in this chapter:
ccf ~ 1 + temperaturewage ~ 1 + sextime ~ 1 + year + sex + year:sex
The ~ symbol (pronounced “tilde” or “wiggle”) divides each statement into two parts. On the left of the tilde is the name of the response variable. On the right is a list of model terms. When there is more than one model term, as is typically the case, the terms are separated by a + sign.
The examples show three types of model terms:
- The symbol
1stands for the intercept term. - A variable name (e.g.,
sexortemperature) stands for using that variable in a main term. - An interaction term is written as two names separated by a colon, for instance
year:sex.
Although this notation looks like arithmetic or algebra, IT IS NOT. The plus sign does not mean arithmetic addition, it simply means that we are “adding another term to the model.”
So in the modeling notation 1 + age does not mean “arithmetically add 1 to the age.” Instead, it means “two model terms: the intercept term and a main term for age.”
Similarly, don’t confuse the tilde with an algebraic equal or minus sign. The model statement is not an equation. So the statement wage ~ 1 + age does not mean “wage equals 1 plus age.” Instead it means, wage is the response variable and there are two model terms: the intercept and a main term for age.”
In order to avoid accidentally leaving out important terms, the modeling notation includes some shorthand. Here are two important parts of this shorthand.
You don’t have to type the 1 term; it will be included by default. So,
wage ~ ageis the same thing aswage ~ 1 + age. On those very rare occasions when you might want to insist that there be no intercept term, you can indicate this with a minus sign:wage ~ age - 1. Think of-1as indicating that we want to remove the intercept term.Almost always, when you include an interaction term between two variables, you will also include the main terms for those variables. The
*sign can be used as shorthand. The modelwage ~ 1 + sex + age + sex:agecan be written simply aswage ~ sex * age.
As you might imagine, it is tricky to include regular arithmetic in model formulas since operators like + and * (and some other operators, too) have special meanings. There are ways to include arithmetic in model formulas, but more often we will do the arithmetic in our data – creating new variables – so we don’t have to do arithmetic inside the model formula. For example, if you wanted to create a model that used gas mileage (in miles per gallon) as an explanatory variable, but your data only had values for distance (in miles) and fuel consumption (in gallons), rather than put this division inside the model, it can be easier to create a new variable – perhaps called mileage or mpg – formed by dividing distance by fuel consumption.